最小二乘法拟合直线

上周面试了一家做机器人的公司，他们发我一道题目，顺便记录学习下。

问题

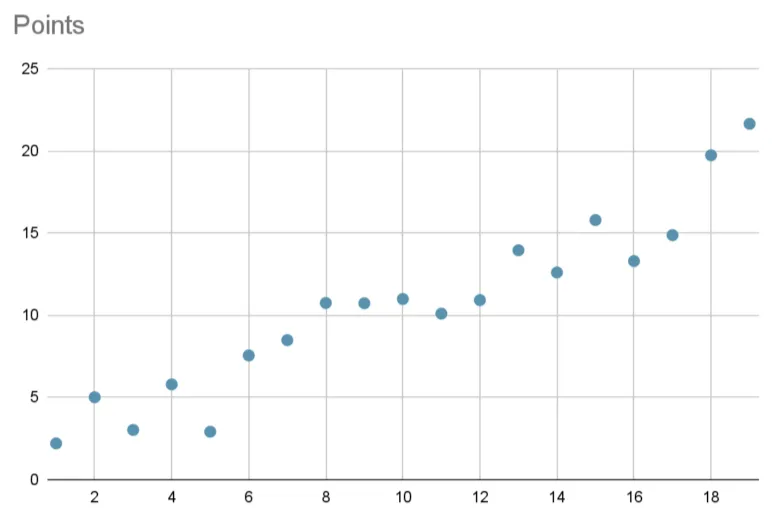
给定一组2D平面上的离散点：请求解出对应拟合直线

要求有几点：
1、建立该问题的数学模型，并且基于C++予以实现，包括：类/接口定义，以及实现细节
2、建议选择如下两种方法之一，或者酌情选择其他的方法：

基于ceres优化库，建立优化问题，并求解
基于Eigen工具库求解（提示：通过特征向量分解的方式）

3、生成测试数据集，并对比验证不同实现的拟合效果
4、输出一份报告，包括：问题的定义，求解细节，以及验证结果等

分析

其实就是直线拟合，这里就想到了最小二乘（视觉SLAM十四讲有写）。

最小二乘法，又称最小平方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。主要作用是从一堆相关数据中求解数据的一般性规律。在图像处理方面多用于各种形状的拟合。

最小二乘拟合直线，主要体现为找到一条直线，使得所有已知的点到这条直线的欧式距离的和最小（或者理解为点到直线的误差平方和最小）。

那我是思考了两种方法，一种是直接求解最小二乘，一种是使用Ceres库优化迭代最小二乘。

解决

数学模型的建立

目标
- 对于等精度测量所得的N组数据，。其中值被认为是准确的，所有误差只与有关。需要把这组观测数据拟合成一条直线，并求对应法向量。
约束
- 要求观测值的偏差的加权平方和为最小，即最小。
变量
- 对于一条直线，有两个待定参数，代表截距，代表斜率（代码里取）。

法一：直接求解

采用直线斜截式，通过最小二乘拟合方程系数

根据最小二乘原理，误差平方和最小，得误差函数：

高数中极值定理可知，误差方程一阶导数等于处取得极值，因此分别对其关于和求导，解,值使得误差函数取最小值。

但是直线斜截式无法表示垂直x轴的直线，如：。

令，得

上面过程繁琐，只适用于直线的最小二乘解。下面将直线斜截式拓展导任意曲线，任意曲线方程

。可以看到直线斜截式即，时的曲线方程。将曲线方程，写成矩阵乘积的形式：

上面乘积形式，即,解出的就是最小二乘解。

代码如下：

void LeastSquares(std::vector<double> &data_x, std::vector<double> &data_y,
                  int data_n) {
  double A, B, C, D, E, F = 0.0;
  double x_square_sum, x_sum, y_sum, xy_multi_sum = 0.0;

  for (int i = 0; i < data_n; i++) {
    x_square_sum += data_x[i] * data_x[i];
    x_sum += data_x[i];
    xy_multi_sum += data_x[i] * data_y[i];
    y_sum += data_y[i];
  }

  // 计算斜率k和截距b
  double k, b, temp = 0;
  if (temp = (data_n * x_square_sum - x_sum * x_sum)) {
    k = (data_n * xy_multi_sum - x_sum * y_sum) / temp;
    b = (x_square_sum * y_sum - x_sum * xy_multi_sum) / temp;
  } else {
    k = 1;
    b = 0;
  }

  // 计算x和y线性相关系数r
  double Xmean, Ymean;
  Xmean = x_sum / data_n;
  Ymean = y_sum / data_n;

  double tempSumXX = 0.0, tempSumYY = 0.0;
  for (int i = 0; i < data_n; i++) {
    tempSumXX += (data_x[i] - Xmean) * (data_x[i] - Xmean);
    tempSumYY += (data_y[i] - Ymean) * (data_y[i] - Ymean);
    E += (data_x[i] - Xmean) * (data_y[i] - Ymean);
  }
  F = sqrt(tempSumXX) * sqrt(tempSumYY);

  double r;
  r = E / F;
  std::cout << "k: " << k << "\n"
            << "b: " << b << "\n"
            << "r: " << r << std::endl;
  // AX + BY + C = 0
  std::cout << "Direction Vector   (B,-A): (" << -1 << "," << -k << ")\n";
  std::cout << "Normal Vector      (A,B): (" << k << "," << -1 << ")\n";

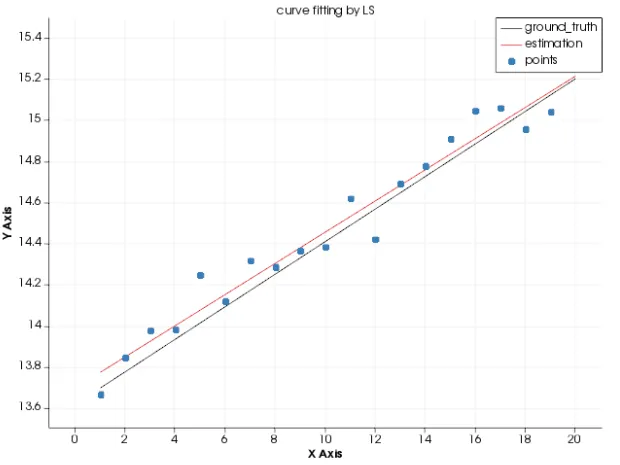
  const char *title = "curve fitting by LS";
  Plot(data_x, data_y, k, b, title);
}

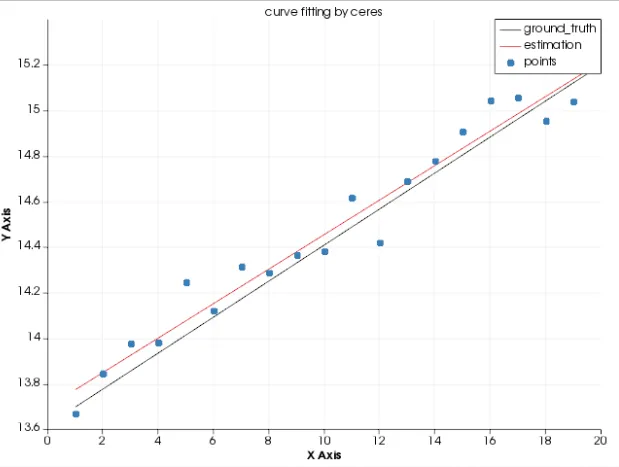
法二：Ceres优化

首先是定义残差快

struct ExponentialResidual {
  ExponentialResidual(double x, double y) : x_(x), y_(y) {}
  template <typename T>
  bool operator()(const T *const k, const T *const b, T *residual) const {
    // r = y - f(x)
    residual[0] = y_ - (k[0] * x_ + b[0]);
    return true;
  }

 private:
  const double x_;
  const double y_;
};

然后构建最小二乘问题

for (int i = 0; i < data_x.size(); ++i) {
    problem.AddResidualBlock(
        new ceres::AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(
            new ExponentialResidual(data_x[i], data_y[i])),
        NULL, &k, &b);
}

最后优化求解

ceres::Solver::Options options;
options.max_num_iterations = 20;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);

结果

Direct_Solution

Ceres_Solution

代码仓库

Least_Square_Fitting_Line

参考

1、最小二乘法求解直线方程系数

2、ceres拟合直线