栈和队列

简介

栈的特点是后入先出。根据这个特点可以临时保存一些数据，之后用到依次再弹出来，常用于 DFS 深度搜索

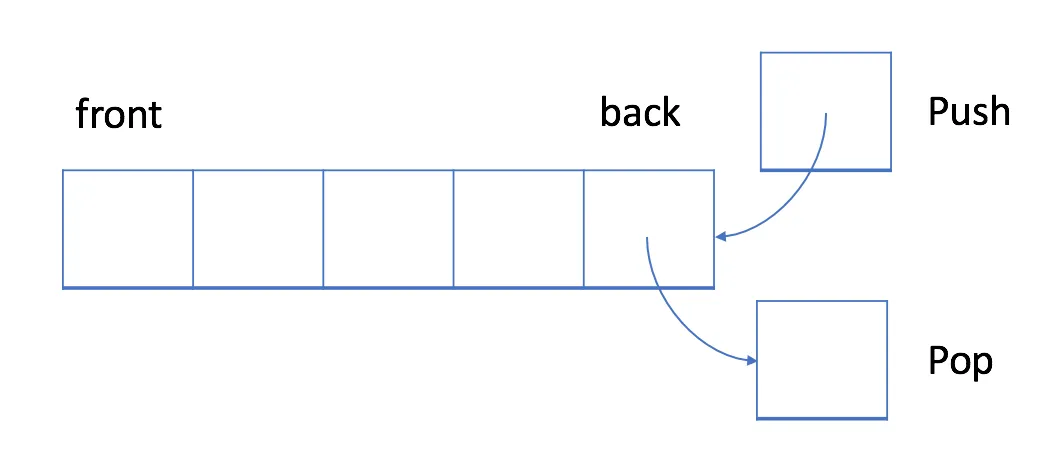
队列一般常用于 BFS 广度搜索，类似一层一层的搜索

Stack 栈

最小栈

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

思路：
用两个栈实现，一个最小栈始终保证最小值在顶部

class MinStack {
 public:
  MinStack() {}

  void push(int val) {
    stack_data.push_back(val);
    if (min_data.empty() || val <= min_data.back()) {
      min_data.push_back(val);
    }
  }
  void pop() {
    if (stack_data.back() == min_data.back()) {
      min_data.pop_back();
    }
    stack_data.pop_back();
  }

  int top() { return stack_data.back(); }

  int getMin() {
    return min_data.back();
    // return *min_element(stack_data.begin(), stack_data.end());
  }

 private:
  vector<int> min_data;
  vector<int> stack_data;
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */

逆波兰表达式求值

波兰表达式计算 -> 输入: [“2”, “1”, “+”, “3”, “*“] -> 输出: 9
解释: ((2 + 1) * 3) = 9

思路：
通过栈保存原来的元素，遇到表达式弹出运算，再推入结果，重复这个过程

class Solution {
 public:
  int evalRPN(const vector<string>& tokens) {
    stack<int> s;
    for (string i : tokens) {
      if (i != "+" && i != "-" && i != "*" && i != "/") {
        s.push(stoi(i));
        continue;
      }
      int tmp2 = s.top();
      s.pop();
      int tmp1 = s.top();
      s.pop();
      if (i == "+")
        s.push(tmp1 + tmp2);
      else if (i == "-")
        s.push(tmp1 - tmp2);
      else if (i == "*")
        s.push(tmp1 * tmp2);
      else if (i == "/")
        s.push(tmp1 / tmp2);
    }
    return s.top();
  }
};

字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。 s = “3[a]2[bc]”, 返回 “aaabcbc”. s = “3[a2[c]]”, 返回 “accaccacc”. s = “2[abc]3[cd]ef”, 返回 “abcabccdcdcdef”.

思路：
通过栈辅助进行操作，这里建了两个栈

class Solution {
 public:
  string decodeString(string s) {
    string res = "";
    stack<int> nums;
    stack<string> strs;
    int num = 0;
    for (int i = 0; i < s.size(); ++i) {
      if (s[i] >= '0' && s[i] <= '9') {
        num = num * 10 + s[i] - '0';
      } else if (s[i] == '[') {
        // 将‘[’前的数字压入nums栈内,字母字符串压入strs栈内
        nums.push(num);
        num = 0;
        strs.push(res);
        res = "";
      } else if (s[i] == ']') {
        // 遇到‘]’时,操作与之相配的‘[’之间的字符,使用分配律
        int times = nums.top();
        nums.pop();
        for (int j = 0; j < times; ++j)
          strs.top() += res;
        res = strs.top();
        strs.pop();
      } else {
        res = res + s[i];
      }
    }
    return res;
  }
};

二叉树的中序遍历

给定一个二叉树，返回它的中序遍历。

思路：
通过stack 保存已经访问的元素，用于原路返回。由于中序遍历是左->根->右，所以要保证有左子树的情况下左子树在栈顶

class Solution {
 public:
  std::vector<int> inorderTraversal(TreeNode* root) {
    std::stack<TreeNode*> s;
    std::vector<int> res;
    while (root || !s.empty()) {
      while (root) {
        s.push(root);
        root = root->left;	// 一直向左
      }
      // 弹出
      root = s.top();
      s.pop();
      res.push_back(root->val);
      root = root->right;
    }
    return res;
  }
};

克隆图

给你无向连通图中一个节点的引用，请你返回该图的深拷贝（克隆）

思路：
由于节点数不会超过100个，所以可以提前创建一个大小为101的 Node * 类型的vector容器nodes，用于存放所有节点。然后通过辅助栈，从给定节点开始遍历原图。
遍历的方法是：从当前节点开始，把它所有的邻居节点入栈。
遍历的过程中，会遇到以下几种情况：

当前节点是第一次被访问。此时nodes中对应的节点的 val 必定还是0（默认构造函数），对nodes中的节点的 val 进行赋值，并把所有的邻居节点push到其neighbors字段中，同时把原图对应的节点入栈。

当前节点已经被访问。判断的依据是nodes数组中的节点 val 已经不是0，直接跳过即可。
等遍历完毕后，nodes存储的就是一张原图的深拷贝，只需要返回初始节点对应的nodes中的节点即可

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
 public:
  Node* cloneGraph(Node* node) {
    if (!node)
      return nullptr;
    stack<Node*> stack;
    vector<Node*> nodes(101);
    for (int i = 0; i < 101; ++i) {
      nodes[i] = new Node();
    }

    stack.push(node);
    while (!stack.empty()) {
      Node* cur = stack.top();
      stack.pop();
      int val = cur->val;
      if (nodes[val]->val == 0) {
        nodes[val]->val = val;
        for (auto n : cur->neighbors) {
          (nodes[val]->neighbors).push_back(nodes[n->val]);
          stack.push(n);
        }
      }
    }
    return nodes[node->val];
  }
};

（未完待续）