二叉树遍历问题

前言

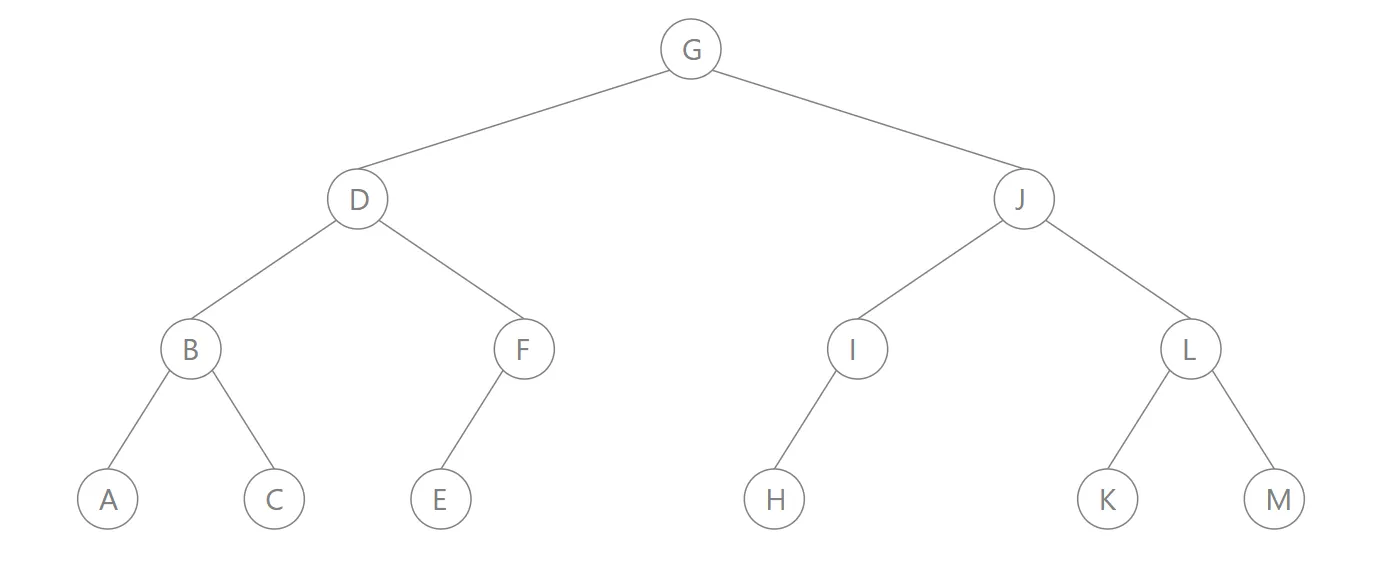
对于下面这个二叉树，不同遍历结果如下：

中序遍历：ABCDEFGHIJKLM
前序遍历：GDBACFEJIHLKM
后序遍历：ACBEFDHIKMLJG

一、二叉树的中序遍历（简）

题目

给定一个二叉树的根节点 root ，返回它的中序遍历。

示例 1：

graph TD
A((1)) --> B(( ))
A((1)) --> C((2))
C((2)) --> F((3))
C((2)) --> G(( ))

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]

提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

题解

中序遍历：左 -> 根 -> 右；前序遍历：根 -> 左 -> 右；后序遍历：左 -> 右 -> 根
二叉树遍历这种，最好是用stack，把需要的入栈，再按条件出栈
比如二叉树如下：

graph TD
A((1)) --> B((2))
A((1)) --> C((3))
B((2)) --> D((4))
B((2)) --> E((5))
C((3)) --> F((6))
C((3)) --> G(( ))
E((5)) --> H((7))
E((5)) --> I((8))

首先每个三角形的节点顺序必须是左根右，比如4->2->5，2->1->3。
中序遍历的过程就是把左侧子树全部入栈，然后一个个出栈，并取值。
这里1<-2<-4入栈，然后4出栈，取值4；到2，2有右子树5，5入栈；
5也执行一遍中序遍历，即左子树7入栈，然后7出栈，取值7；到5，5有右子树8，8入栈。
重复直到没有子树

struct TreeNode {
  int val;
  TreeNode* left;
  TreeNode* right;
  TreeNode() : val(0), left(nullptr), right(nullptr) {}
  explicit TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  TreeNode(int x, TreeNode* left, TreeNode* right)
      : val(x), left(left), right(right) {}
};

class Solution {
 public:
  std::vector<int> inorderTraversal(TreeNode* root) {
    vector<int> res;
    if (root == NULL)
      return res;
    stack<TreeNode*> s;
    TreeNode* cur = root;
    while (cur || !s.empty()) {
      if (cur) {
        s.push(cur);
        cur = cur->left;  // left
      } else {
        cur = s.top();
        s.pop();
        res.push_back(cur->val);  // root
        cur = cur->right;         // right
      }
    }
    return res;
  }
};

二、二叉树的前序遍历（简）

题目

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

graph TD
A((1)) --> B(( ))
A((1)) --> C((2))
C((2)) --> F((3))
C((2)) --> G(( ))

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]

示例 4：

graph TD
A((1)) --> B((2))
A((1)) --> C(( ))

输入：root = [1,2]
输出：[1,2]

示例 5：

graph TD
A((1)) --> B(( ))
A((1)) --> C((2))

输入：root = [1,null,2]
输出：[1,2]

提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

题解

首先每个三角形的节点顺序必须是根左右，比如2->4->5，1->2->3。
参考中序遍历，中序遍历是左根右，所以要左子树入栈->出栈->取值->判断右子树；
而先序遍历是根左右，所以要取值->左子树入栈->出栈->判断右子树

class Solution {
 public:
  vector<int> preorderTraversal(TreeNode* root) {
    vector<int> res;
    if (root == NULL)
      return res;
    stack<TreeNode*> s;
    TreeNode* cur = root;
    while (cur || !s.empty()) {
      if (cur) {
        res.push_back(cur->val);  // root
        s.push(cur);
        cur = cur->left;  // left
      } else {
        cur = s.top();
        s.pop();
        cur = cur->right;  // right
      }
    }
    return res;
  }
};

三、二叉树的后序遍历（简）

题目

给你一棵二叉树的根节点 root ，返回其节点值的后序遍历。

示例 1：

graph TD
A((1)) --> B(( ))
A((1)) --> C((2))
C((2)) --> F((3))
C((2)) --> G(( ))

输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [1]
输出：[1]

提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

题解1

首先每个三角形的节点顺序必须是左右根，比如4->5->2，2->3->1。
参考前序遍历的根左右，输出根右左，然后倒序，就是左右根

class Solution {
 public:
  vector<int> postorderTraversal(TreeNode* root) {
    vector<int> res;
    if (root == NULL)
      return res;
    stack<TreeNode*> s;
    TreeNode* cur = root;
    while (cur || !s.empty()) {
      if (cur) {
        res.push_back(cur->val);  // root
        s.push(cur);
        cur = cur->right;  // right
      } else {
        cur = s.top();
        s.pop();
        cur = cur->left;  // left
      }
    }
    reverse(res.begin(), res.end());
    return res;
  }
};

题解2

顺便记录下递归的写法

class Solution {
 public:
  void postorder(TreeNode* root, vector<int>& res) {
    if (root == nullptr) {
      return;
    }
    postorder(root->left, res);
    postorder(root->right, res);
    res.push_back(root->val);
  }

  vector<int> postorderTraversal(TreeNode* root) {
    vector<int> res;
    postorder(root, res);
    return res;
  }
};

四、二叉树的层序遍历（中）

题目

给你二叉树的根节点 root ，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

示例 1：

graph TD
A((3)) --> B((9))
A((3)) --> C((20))
C((20)) --> F((15))
C((20)) --> G((7))

输入：root = [3,9,20,null,null,15,7]
输出：[ [3],[9,20],[15,7] ]

示例 2：
输入：root = [1]
输出：[1]

示例 3：
输入：root = []
输出：[]

提示：
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

题解

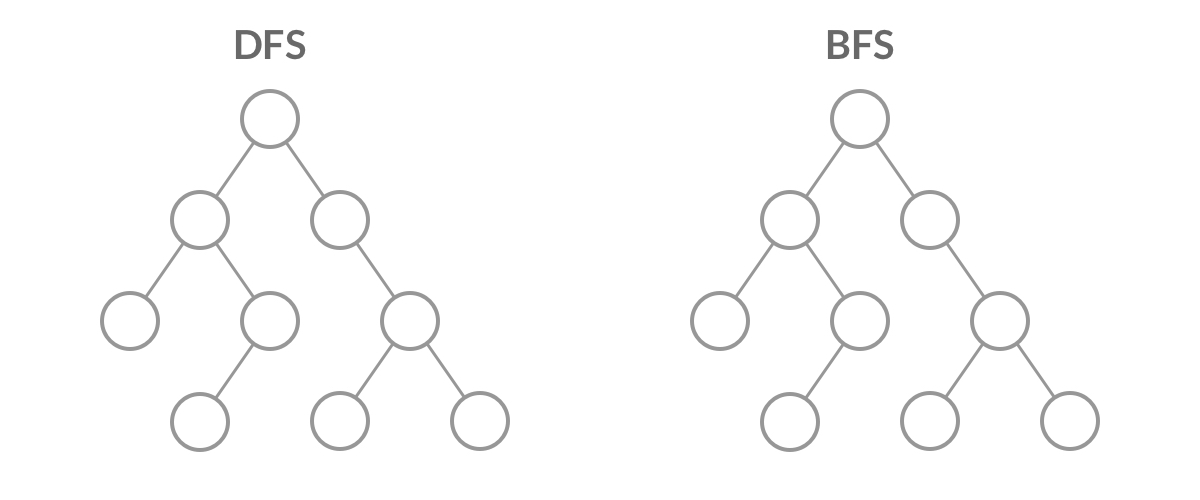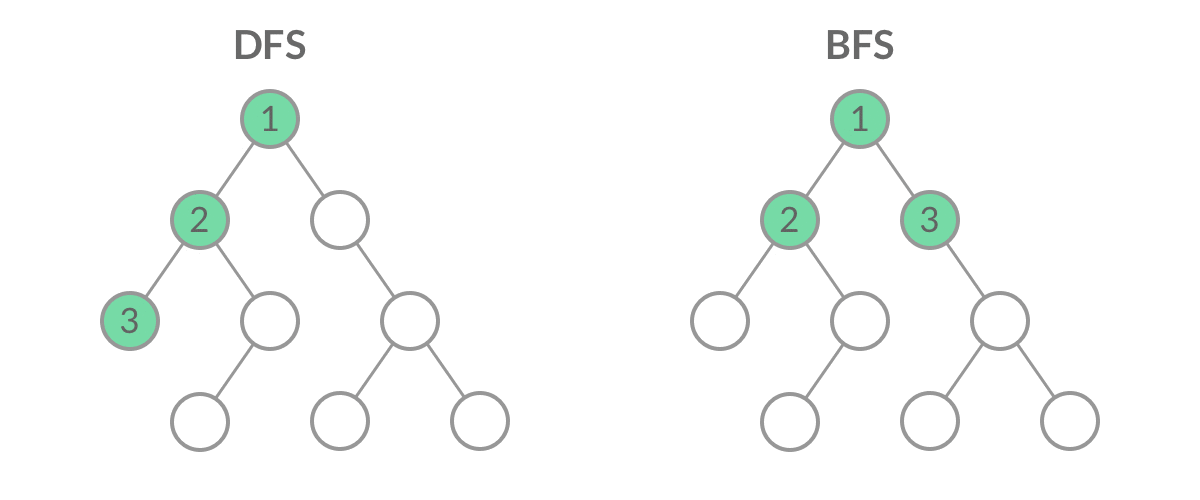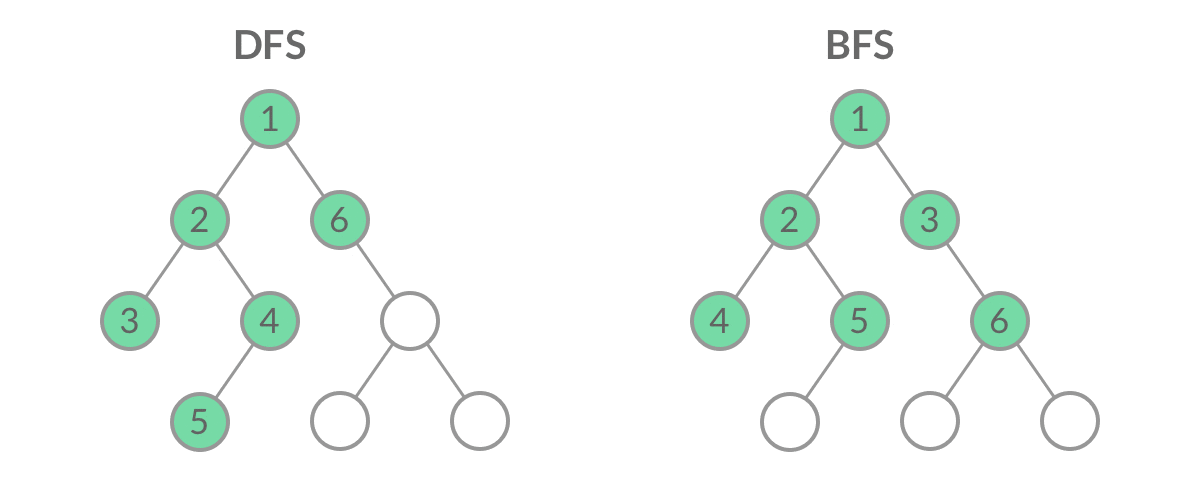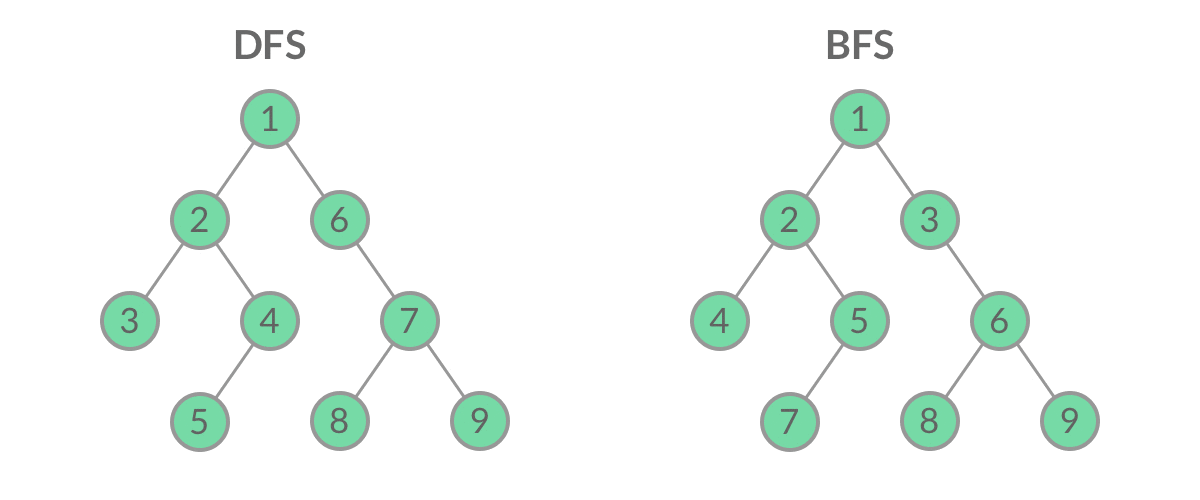
首先要知道遍历二叉树，DFS和BFS的顺序是不一样的
DFS_BFS
从gif图可以看出，前中后序遍历就是DFS遍历，层序遍历就类似BFS遍历，不同的是BFS是输出一个一维数组，而层序遍历要求我们区分每一层，也就是返回一个二维数组
那首先我们可以先实现BFS遍历，用队列来存储遍历的节点，因为队列是先进先出，顺序不会乱

// 二叉树的BFS遍历
class Solution {
 public:
  vector<int> levelOrder(TreeNode* root) {
    vector<int> res;
    queue<TreeNode*> q;
    if (root != NULL) {
      q.push(root);
    }
    while (!q.empty()) {
      TreeNode* node = q.front();
      q.pop();
      res.push_back(node->val);
      if (node->left != NULL) {
        q.push(node->left);
      }
      if (node->right != NULL) {
        q.push(node->right);
      }
    }
    return res;
  }
};

有了BFS遍历，怎么把每一层的分别记录下来呢
很简单，在每一层遍历开始前，先记录队列中的结点数量n（也就是这一层的结点数量），然后一口气处理完这一层的n个结点

class Solution {
 public:
  vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> res;
    queue<TreeNode*> q;
    if (root != NULL) {
      q.push(root);
    }
    while (!q.empty()) {
      int n = q.size();
      vector<int> temp;
      for (int i = 0; i < n; i++) {
        TreeNode* node = q.front();
        q.pop();
        temp.push_back(node->val);
        if (node->left != NULL) {
          q.push(node->left);
        }
        if (node->right != NULL) {
          q.push(node->right);
        }
      }
      res.push_back(temp);
    }
    return res;
  }
};