前言

排序算法面试中经常被考到，这里对排序算法做一次总结，方便巩固复习。

名称 时间 空间 说明
冒泡排序 1 按顺序依次两个比较，通过交换位置保证大的排后面，依次循环
选择排序 1 选出最小的数，放在首位；再次选，放在第二位
快速排序 1 先选择中间值，然后把比它小的放在左边，大的放在右边（具体实现就是从两边找，找到一对后交换）；然后分别对两边重复进行上述操作
堆排序 1 利用堆的性质进行的选择排序
插入排序 1 逐一取出元素，在已经排序的元素序列中从后向前扫描，放到适当的位置
希尔排序
1 选择一个步长，然后按间隔为步长的单元进行排序，递归，步长逐渐变小，直至为1
归并排序 n 逐层对半拆分，然后逐层从最小分组开始排序，合并成大的分组

冒泡排序

算法原理

1、遍历数组，从左到右，若右边的数比左边的大，则交换；
2、第一遍：最大的数沉下去；
3、第二遍：第二大的数沉在倒数第二个位置。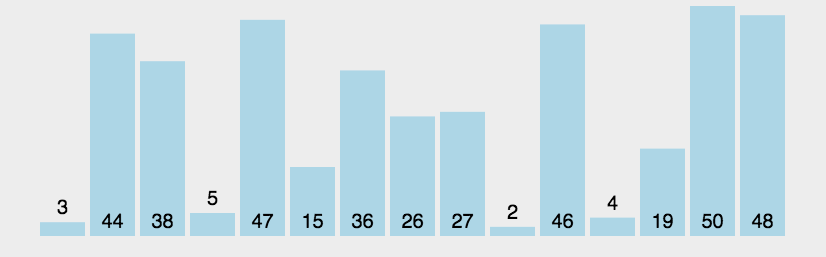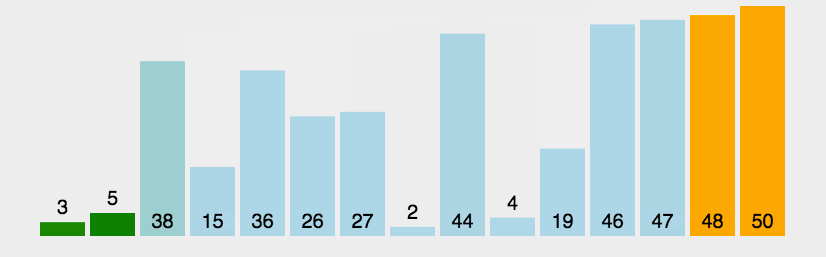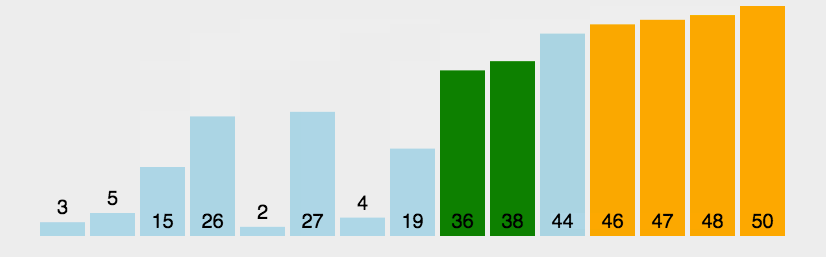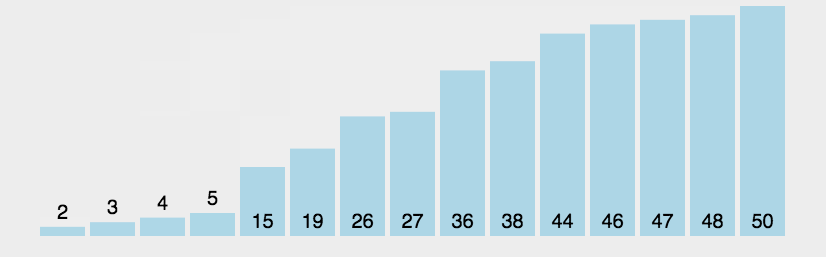
bubble_sort

复杂度

时间复杂度最差是，最优是
两层循环，最差循环次数是，也就是
属于稳定排序
注：稳定排序：排序前后两个相等的数相对位置不变，则算法稳定；
非稳定排序：排序前后两个相等的数相对位置发生了变化，则算法不稳定
比如[5,5,1,4,3]，排序后第一个5还是在前，第二个5还是在后，即稳定

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 这个排序次数是固定的，不论元素排列怎么样，时间复杂度都是O(n^2)
void BubbleSort(vector<int>& nums) {
  int n = nums.size();
  for (int i = n - 1; i > 0; i--) {
    for (int j = 0; j < i; j++) {
      if (nums[j] > nums[j + 1]) {
        // 交换
        int temp = nums[j];
        nums[j] = nums[j + 1];
        nums[j + 1] = temp;
      }
    }
  }
}

// 优化，比如[1,2,3,5,4]，只需要遍历一趟即可
void BubbleSort_2(vector<int>& nums) {
  int n = nums.size();
  bool flag = false;  // 无序
  for (int i = n - 1; i > 0 && !flag; i--) {
    flag = true;  // 有序
    for (int j = 0; j < i; j++) {
      if (nums[j] > nums[j + 1]) {
        // 交换
        int temp = nums[j];
        nums[j] = nums[j + 1];
        nums[j + 1] = temp;
        flag = false;  // 无序
      }
    }
  }
}

选择排序

算法原理

1、线性遍历数组，选出最小的数，放在第一个位置；
2、然后，选出第二小的数，放在第二个位置。依此类推。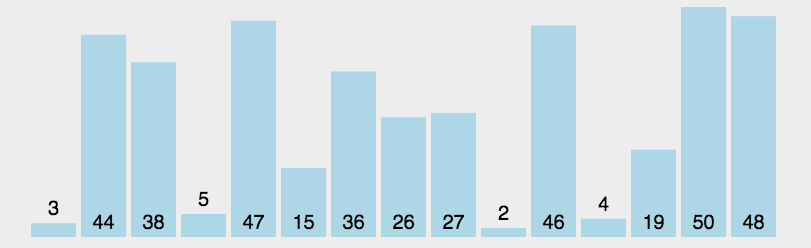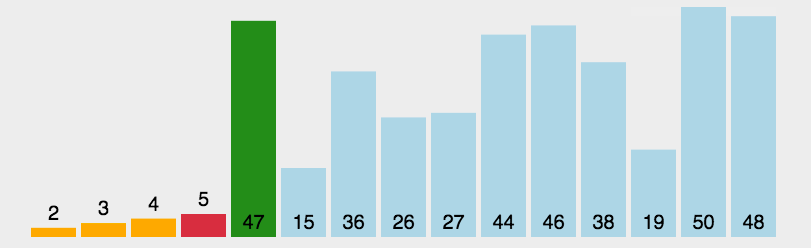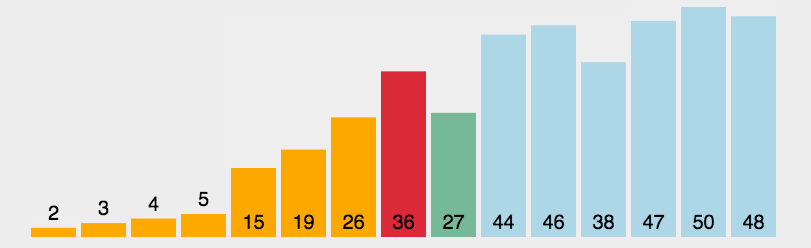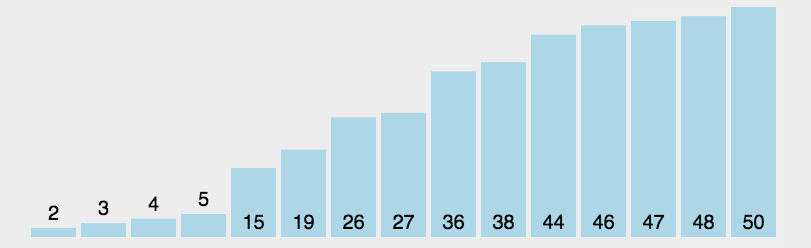
selection_sort

复杂度

时间复杂度最差是，最优也是
两层循环，最差循环次数是，也就是
属于不稳定排序

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void SelectSort(vector<int> & nums) {
  int n = nums.size();
  for (int i = 0; i < n; i++) {
    // 找到从i开始到最后一个元素中最小的元素,k存储最小元素的下标.
    int k = i;
    for (int j = i + 1; j < n; j++) {
      if (nums[j] < nums[k]) {
        k = j;
      }
    }
    // 将最小的元素a[k]和开始的元素a[i]交换数据
    if (k != i) {
      int temp;
      temp = nums[k];
      nums[k] = nums[i];
      nums[i] = temp;
    }
  }
}

快速排序

算法原理

1、确定一个分界点；
2、调整区间：使得左边所有值 <= 分界点， 右边所有值 >= 分界点；
3、递归处理左右两段。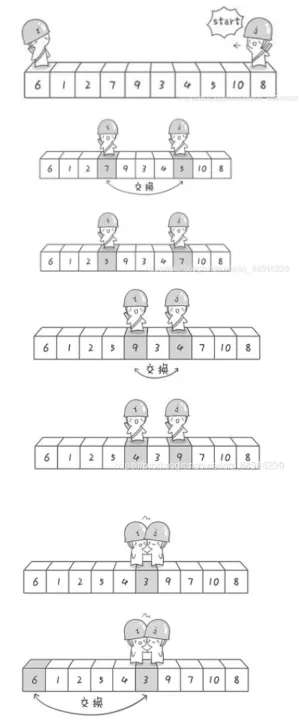
quicksort_4

复杂度

时间复杂度最差是，最优是
属于不稳定排序
和归并相比，都是分治思想，但归并是稳定的，他是不稳定的

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/* 看上面的图示, i 从左边移动, j 从右边移动,以最左边作为基准数 pivot ,所以先是 j 移动
 * 这里排小到大, ve[j] 比 pivot 大的, j 左移,否则停下; ve[i] 比 pivot 小的, i 右移,否则停下
 * j 和 i 都停下后, ve[j] 和 ve[i] 互换,继续上面的移动
 * 直到 j 和 i 相碰后,都停下, pivot 和 ve[i] 互换
 * 至此,第一轮探测结束, pivot 左边数字均 ≤ pivot,右边数字均 ≥ pivot
 * 然后我们可以分开左右两边,又按照上述方法排序
 */
void QuickSort(vector<int>& nums, int left, int right) {
  if (left >= right) {
    // 如果左边界大于等于右边界，直接返回
    return;
  }
  int pivot = nums[left]; // 选取第一个元素作为基准值
  int i = left, j = right;  // 定义左右指针
  while (i < j) { // 双指针遍历数组
    while (i < j && nums[j] >= pivot) {
      // 从右往左找到第一个小于基准值的元素
      j--;
    }
    while (i < j && nums[i] <= pivot) {
      // 从左往右找到第一个大于基准值的元素
      i++;
    }
    // 将左边大于基准值的元素和右边小于基准值的元素交换
    std::swap(nums[i], nums[j]);
  }
  // 这时nums[i]是小于基准值的元素,跟基准值交换,就可以将基准值放到中间
  std::swap(nums[left], nums[i]);
  QuickSort(nums, left, i - 1);
  QuickSort(nums, j + 1, right);
}

int main() {
  vector<int> ve = {6, 1, 2, 7, 9, 3, 4, 5, 10, 8};
  QuickSort(ve, 0, ve.size() - 1);
  for (auto i : ve) {
    cout << i << " ";
  }
  return 0;
}

堆排序

算法原理

1、将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点；
2、将其与末尾元素进行交换，此时末尾就为最大值；
3、然后将剩余 n-1 个元素重新构造成一个堆，这样会得到n个元素的次小值；
4、如此反复执行，便能得到一个有序序列了
注：升序采用大顶堆，降序采用小顶堆

复杂度

时间复杂度最差是，最优是
属于不稳定排序
详见堆排序

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
void display(int array[], int size) {
  for (int i = 0; i < size; i++) {
    printf("%d ", array[i]);
  }
  printf("\n");
}

void swap(int array[], int x, int y) {
  int temp = array[x];
  array[x] = array[y];
  array[y] = temp;
}

// 向下调整算法
void adjust_down(int array[], int i, int n) {
  int parent = i;         // 父节点下标
  int child = 2 * i + 1;  // 子节点下标
  while (child < n) {
    if (child + 1 < n && array[child] > array[child + 1]) {
      // 选出左右child小的那个，与parent比较
      child++;
    }
    if (array[child] < array[parent]) {
      // 如果child比parent小,交换parent和child,这样就保证parent比左右child都小
      swap(array, parent, child);  // 交换parent和child
      parent = child;              // child下标赋给parent下标
    } else {
      break;
    }
    child = child * 2 + 1;  // 换行,比较下一层的parent和child
  }
}

// 向上调整算法
void adjust_up(int array[], int i, int n) {
  int parent = i;         // 父节点下标
  int child = 2 * i + 1;  // 子节点下标
  while (child < n) {
    if (child + 1 < n && array[child] < array[child + 1]) {
      // 选出左右child大的那个，与parent比较
      child++;
    }
    if (array[parent] < array[child]) {
      // 如果parent比child小,交换parent和child,这样就保证parent比左右child都大
      swap(array, parent, child);  // 交换parent和child
      parent = child;              // child下标赋给parent下标
    } else {
      break;
    }
    child = child * 2 + 1;  // 换行,比较下一层的parent和child
  }
}

// 创建小顶堆
void BuildMinHeap(int array[], int size) {
  for (int i = size / 2 - 1; i >= 0; i--) {
    // 倒数第二排开始,对每一个三角形成的堆,创建小顶堆
    adjust_down(array, i, size);
  }
}

// 创建大顶堆
void BuildMaxHeap(int array[], int size) {
  for (int i = size / 2 - 1; i >= 0; i--) {
    // 倒数第二排开始,对每一个三角形成的堆,创建大顶堆
    adjust_up(array, i, size);
  }
}

// 降序
void MaxHeapSort(int array[], int size) {
  BuildMinHeap(array, size);  // 创建小顶堆
  display(array, size);
  for (int i = size - 1; i > 0; i--) {
    swap(array, 0, i);
    // 这里交换顶点和第i个数据,就是把顶点的最小值存到尾部,
    // 在剩余的数字中再进行向下调整,重新建立小顶堆
    adjust_down(array, 0, i);
  }
}

// 升序
void MinHeapSort(int array[], int size) {
  BuildMaxHeap(array, size);  // 创建大顶堆
  display(array, size);
  for (int i = size - 1; i > 0; i--) {
    // 这里交换顶点和第i个数据,就是把顶点的最大值存到尾部,
    // 在剩余的数字中再进行向上调整,重新建立大顶堆
    swap(array, 0, i);
    adjust_up(array, 0, i);
  }
}

int main() {
  int array[] = {49, 38, 65, 97, 76, 13, 27, 49, 10};
  int size = sizeof(array) / sizeof(int);

  // 打印数据
  display(array, size);
  MaxHeapSort(array, size);
  display(array, size);

  return 0;
}

插入排序

算法原理

对于数组a[10]，
1、把a[0]认为已经排好序的；
2、从a[1]开始向前和已经排好序的对比，小于排好的就调换，否则停止，并认为a[0,1]已经排好；
3、然后a[2]又开始按步骤2进行，一直到a[10]。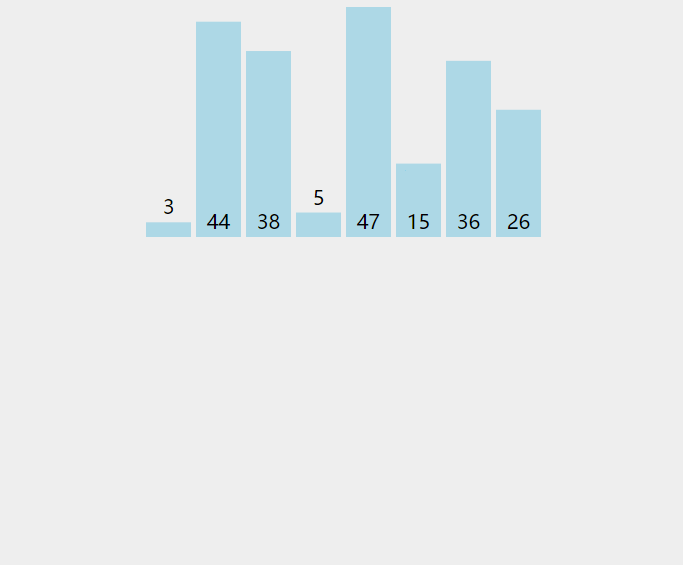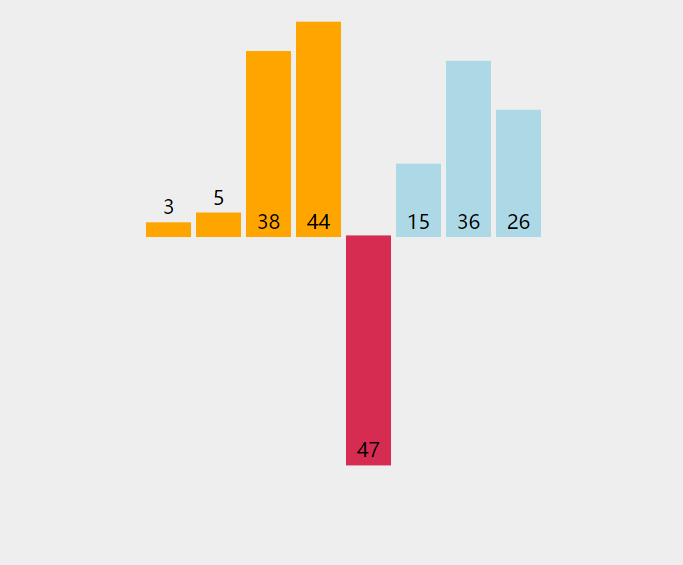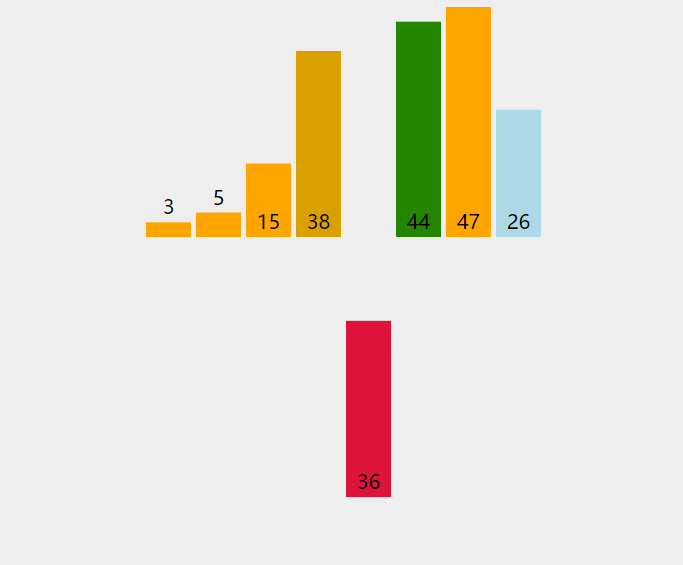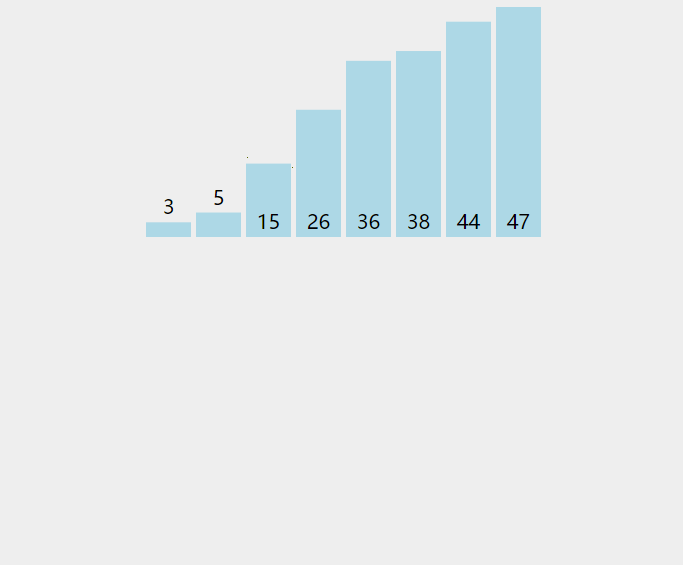
insertion_sort

复杂度

时间复杂度最差是，最优是
两层循环，最差循环次数是，也就是
属于稳定排序

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void InsertSort(vector<int>& nums) {
  int n = nums.size();
  // 间隔为1，对数组从第2位开始，记为key；
  // 按间隔依次比较前面的元素，比key大就放到key后面；
  // 一个key比较完后，key=key+1，继续比较
  int gap = 1;
  for (int i = 0; i < gap; i++) {
    for (int j = i + gap; j < n; j = j + gap) {
      int key = nums[j];
      int k = j - gap;
      while (k >= 0 && nums[k] > key) {
        nums[k + gap] = nums[k];
        k = k - gap;
      }
      nums[k + gap] = key;
    }
  }
}

希尔排序

算法原理

希尔排序又称 “缩小增量排序”，它也是一种插入类排序的方法。
希尔排序属于插入类排序，是将整个有序序列分割成若干小的子序列分别进行插入排序。
其实和插入排序一样，只不过比较间隔不局限于1，而是 n/2，其余都一样。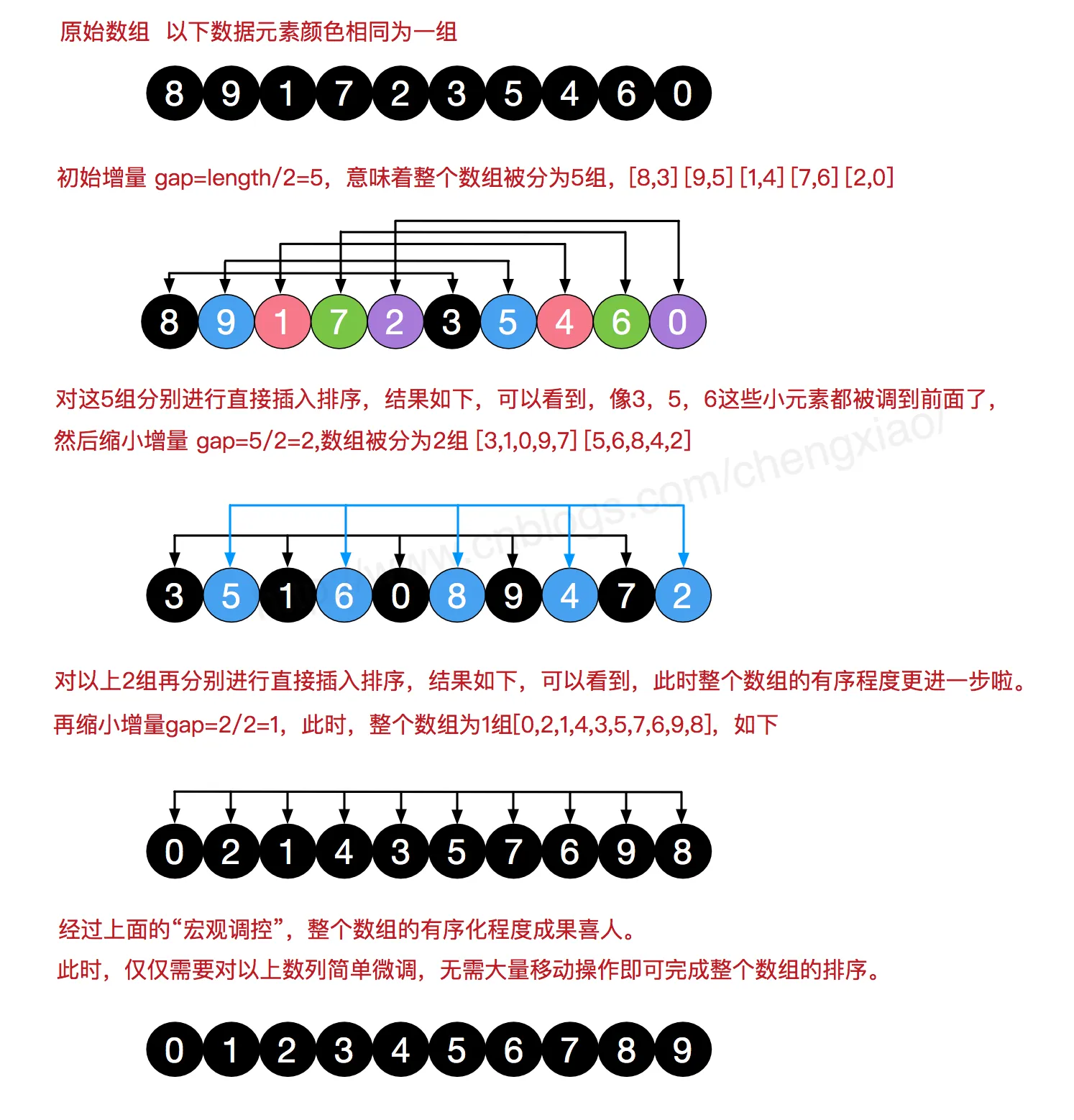
shell_sort

复杂度

时间复杂度是，
属于不稳定排序

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void ShellSort(vector<int>& nums) {
  int n = nums.size();
  // 这里d=n/2,插入排序d=1
  for (int gap = n / 2; gap >= 1; gap = gap / 2) {  // 将数组分割为多个子表
    for (int i = 0; i < gap; i++) {                 // 依次处理子表
      for (int j = i + gap; j < n; j = j + gap) {  // 按间隔处理子表
        int key = nums[j];
        int k = j - gap;
        while (k >= 0 && nums[k] > key) {
          nums[k + gap] = nums[k];
          k = k - gap;
        }
        nums[k + gap] = key;
      }
    }
  }
}

归并排序

算法原理

1、确定分界点mid = (left + right)>>1，逐层折半分组；
2、然后从最小分组开始比较排序，合并成一个大的分组，逐层进行；
3、最终所有的元素都是有序的。
注：>>1：除以2取整（进1法），<<1：乘以2取整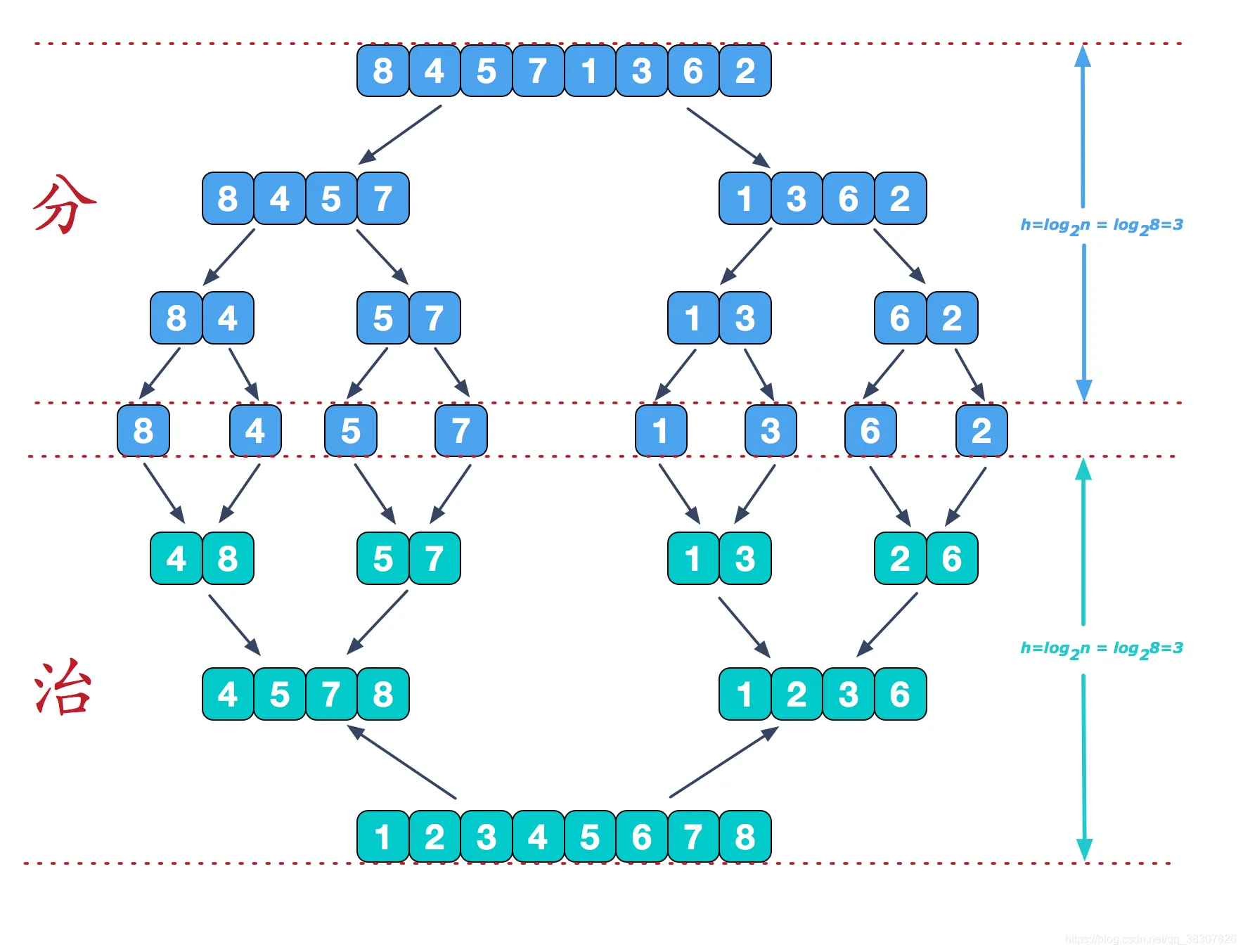
merge_sort1
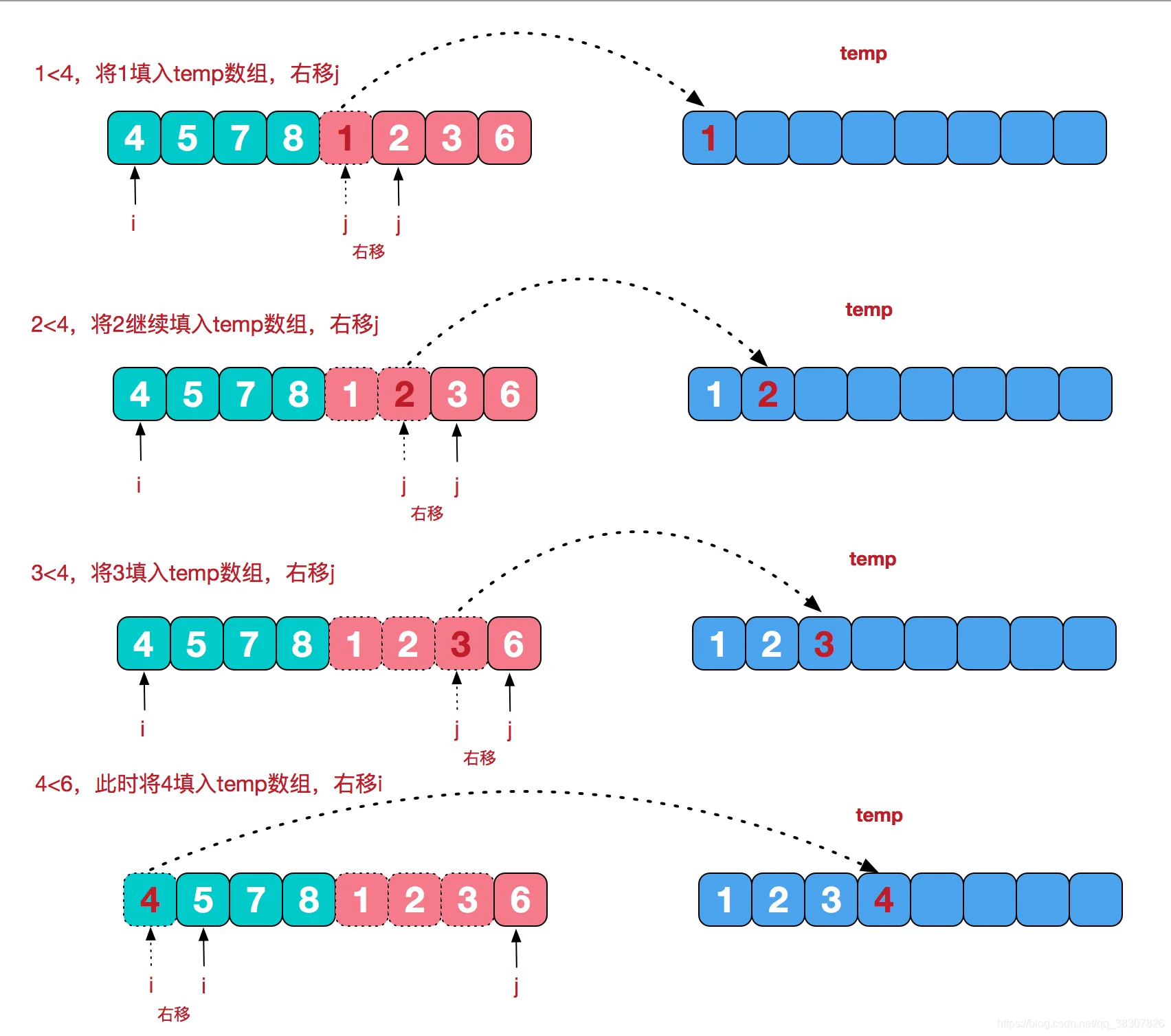
merge_sort2

复杂度

时间复杂度最差是，最优是
假设待排序的数组元素个数为n，设高度为x，x意味着n个元素需要连续二分x次才剩下1个元素，即，），每一层的总比较次数为n，所以时间复杂度为
属于稳定排序

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
void MergeSort(vector<int>& nums, int left, int right) {
  if (left >= right) {
    return;
  }
  vector<int> tmp;
  int mid = left + right >> 1;
  // 分别对左边和右边排序，对应归并里的分
  MergeSort(nums, left, mid);
  MergeSort(nums, mid + 1, right);

  /*对应归并里的合
  * 可以这么理解，当left >= right后，就是数组拆分完了，下面是进行合并操作；
  * tmp数组是用来存储每次排序后的结果，然后赋值会给原数组，
  * 这样每次合并前的左右两边都是排好序的，我们只需要比较左右两边即可；
  * 比如[7, 8, 11, 12]和[3, 9]排序；
  * 7和3比，3存入tmp；7和9比，7存入tmp；8和9比，8存入tmp；11和9比，9存入tmp；
  * 最后剩下[11, 12]，直接存入tmp
  */
  int i = left, j = mid + 1;
  while (i <= mid && j <= right) {
    if (nums[i] <= nums[j]) {
      tmp.push_back(nums[i]);
      i++;
    } else {
      tmp.push_back(nums[j]);
      j++;
    }
  }
  while (i <= mid) {
    tmp.push_back(nums[i]);
    i++;  // 只要左边没循环完，就执行此操作
  }
  while (j <= right) {
    tmp.push_back(nums[j]);
    j++;  // 只要右边没循环完，就执行此操作
  }
  for (i = left, j = 0; i <= right; i++, j++) {
    nums[i] = tmp[j];  // 再将临时数组放回原数组
  }
}

int main() {
  vector<int> ve = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
  MergeSort(ve, 0, ve.size() - 1);
  for (auto i : ve) {
    cout << i << " ";
  }
  return 0;
}
License

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

Share

快来参与讨论吧~

BlogCategoriesTagsArchives
ProjectIMU_PreintegrationLeGO_LOAM
SocialFriendCircleCommentsTravelling
MoreHomePageAbout
©2018 - Felicx 使用 Stellar 创建
总访问 113701 次 | 本页访问 326 次
共发表 83 篇Blog · 总计 127.5k 字