前言

我们知道，DFS通常是在树或者图结构上进行的，而岛屿问题都是网格，能不能用DFS呢？
可以，记住，凡是网格的都应该想到用DFS，岛屿问题就是一类典型的网格问题。

一、岛屿数量（中）

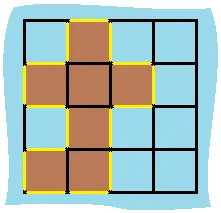
题目

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：





输出：1

示例 2：
输入：





输出：3

提示：



的值为或

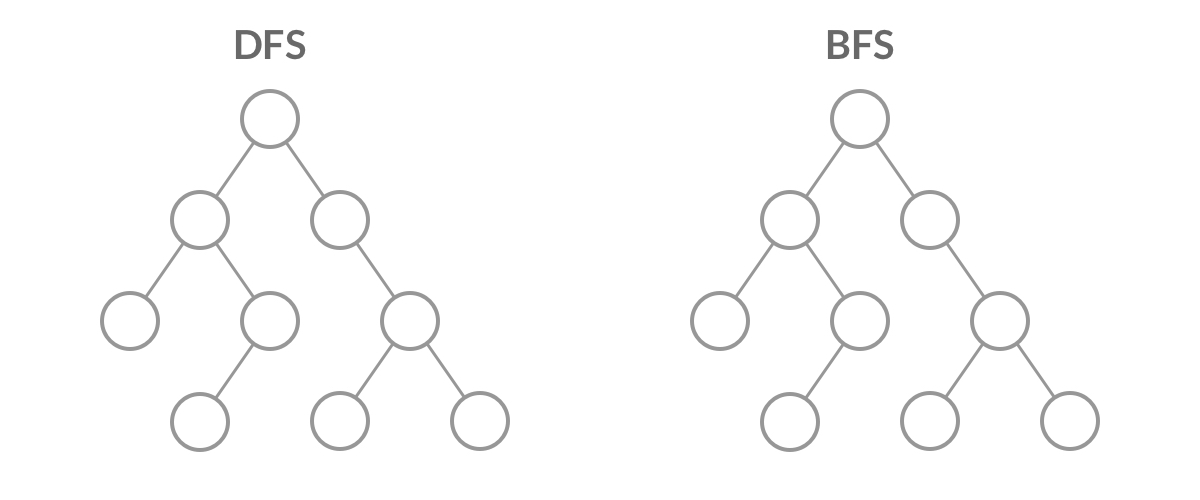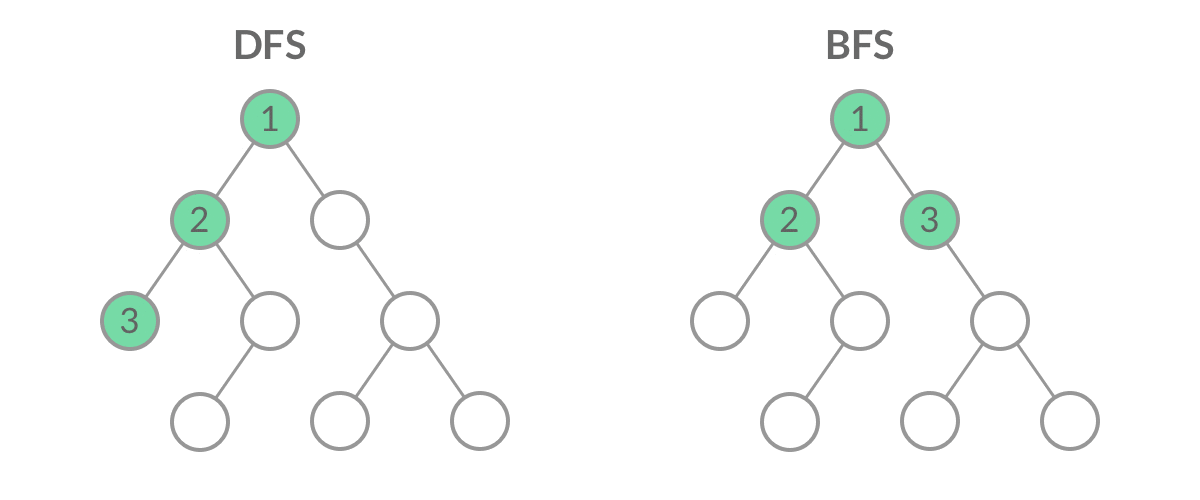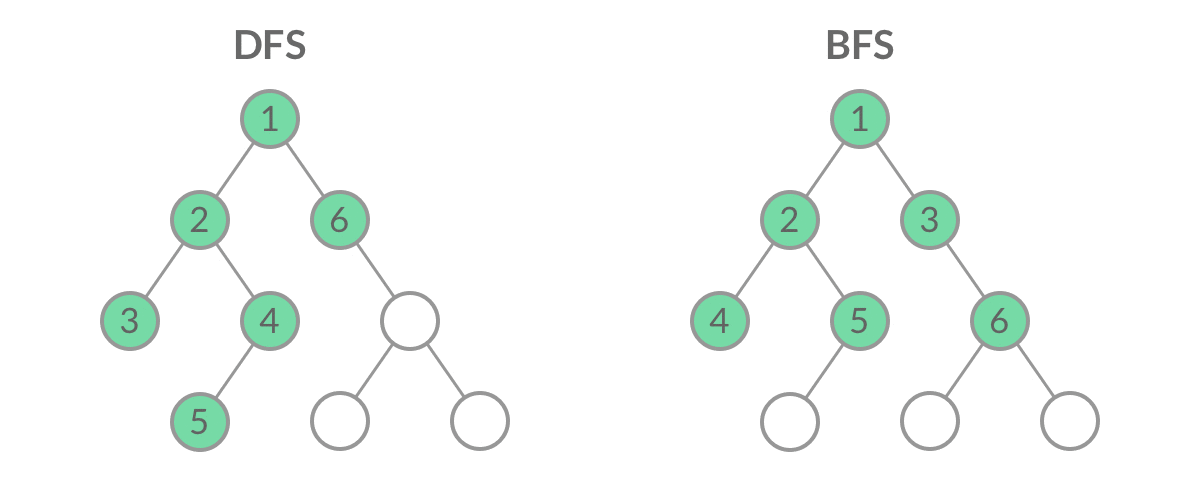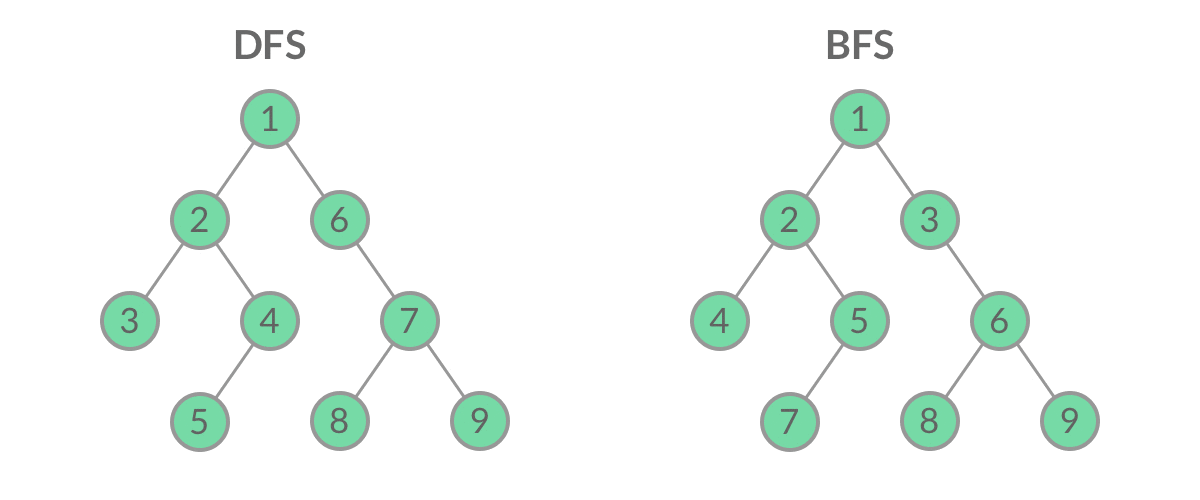
题解

首先我们要清楚DFS的基本结构，先看简单的二叉树DFS遍历结构

1
2
3
4
5
6
7
8
9
void traverse(TreeNode* root) {
  // 判断base case
  if (root == NULL) {
    return;
  }
  // 访问两个相邻结点:左子结点,右子结点
  traverse(root->left);
  traverse(root->right);
}

可以看到，二叉树的DFS有两个要素：访问相邻结点、判断base case。

  • 二叉树的相邻结点非常简单，只有左子结点和右子结点两个。
    • 二叉树本身就是一个递归定义的结构：一棵二叉树，它的左子树和右子树也是一棵二叉树。那么我们的DFS遍历只需要递归调用左子树和右子树即可。
  • 二叉树遍历的base case是root == NULL。
    • 这样一个条件判断其实有两个含义：一方面，这表示 root 指向的子树为空，不需要再往下遍历了。另一方面，在root == NULL的时候及时返回，可以让后面的root->left和root->right操作不会出现空指针异常。

那么对于网格上的DFS，我们完全可以参考二叉树的DFS，写出网格DFS的两个要素。

  • 首先看相邻结点。很明显，网格结构中的格子的相邻结点是上下左右四个，即(row-1, col),(row+1, col),(row, col-1),(row, col+1)；
  • 然后是base case。根据二叉树的对应过来，是超出网格范围的格子，即row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0。

根据分析，可以得出网格DFS遍历的框架代码：

1
2
3
4
5
6
7
8
9
10
11
void dfsGrid(vector<vector<char>>& grid, int row, int col) {
  if (row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0) {
    // 防止row和col越界(上下左右)
    return;
  }

  dfsGrid(grid, row - 1, col);  // 上
  dfsGrid(grid, row + 1, col);  // 下
  dfsGrid(grid, row, col - 1);  // 左
  dfsGrid(grid, row, col + 1);  // 右
}

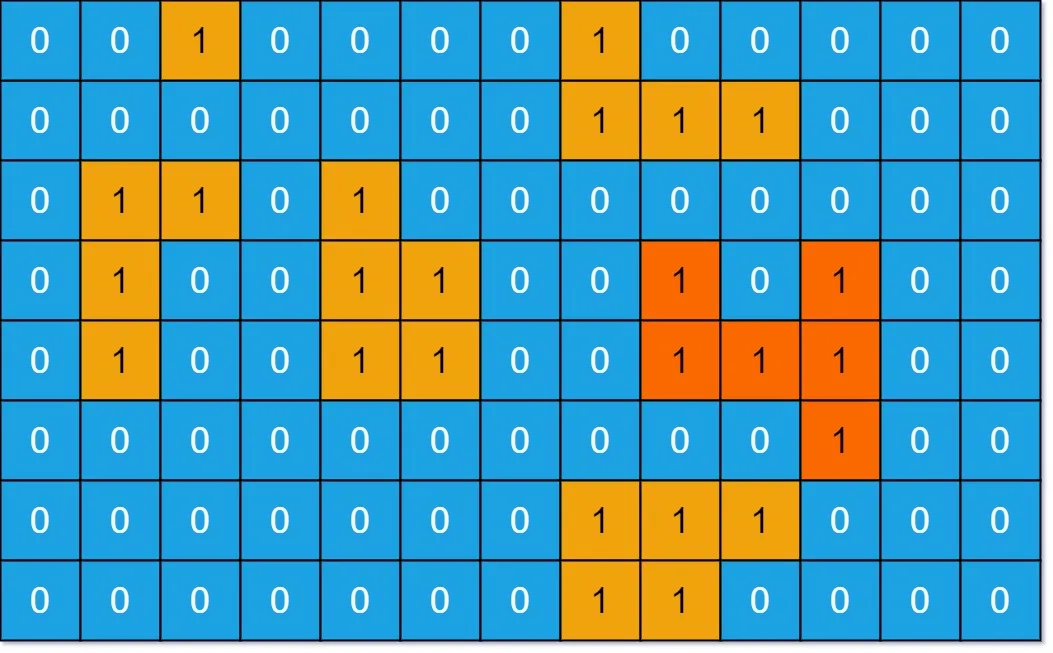
这里有个问题，怎么避免重复值，比如下面这张图，dfsGrid遍历时会一直在这里不断循环。
grid_DFS
简单的方法就是标记已经遍历过的格子。比如岛屿问题，把走过的陆地格子的值改为2。这样就能得到一个网格DFS遍历的通用框架代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void dfsGrid(vector<vector<char>>& grid, int row, int col) {
  if (row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0) {
    // 防止row和col越界(上下左右)
    return;
  }

  if (grid[row][col] != '1') {
    // 遍历到海洋或者已经遍历过的陆地,退出
    return;
  }

  grid[row][col] = '2';         // 去重,防止多次遍历
  dfsGrid(grid, row - 1, col);  // 上
  dfsGrid(grid, row + 1, col);  // 下
  dfsGrid(grid, row, col - 1);  // 左
  dfsGrid(grid, row, col + 1);  // 右
}

有了网格DFS遍历的通用框架，我们只需要用两层for循环遍历整张二维表格中所有的陆地，连续的视为一个岛屿。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
 public:
  int numIslands(vector<vector<char>>& grid) {
    int res = 0;
    // 两层for循环,遍历整张二维表格中所有的陆地,i是行,j是列
    for (int i = 0; i < grid.size(); i++) {
      for (int j = 0; j < grid[0].size(); j++) {
        if (grid[i][j] == '1') {
          dfsGrid(grid, i, j);  // 深度递归，遍历所有的陆地
          res++;
        }
      }
    }
    return res;
  }

  void dfsGrid(vector<vector<char>>& grid, int row, int col) {
    if (row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0) {
      // 防止row和col越界(上下左右)
      return;
    }

    if (grid[row][col] != '1') {
      // 遍历到海洋或者已经遍历过的陆地,退出
      return;
    }

    grid[row][col] = '2';         // 去重,防止多次遍历
    dfsGrid(grid, row - 1, col);  // 上
    dfsGrid(grid, row + 1, col);  // 下
    dfsGrid(grid, row, col - 1);  // 左
    dfsGrid(grid, row, col + 1);  // 右
  }
};

二、岛屿的周长（简）

题目

给定一个row x col的二维网格地图grid，其中：grid[i][j] = 1表示陆地，grid[i][j] = 0表示水域。

网格中的格子水平和垂直方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例 1：
island-perimeter
输入：
输出：16
解释：它的周长是上面图片中的 16 个黄色的边

示例 2：
输入：grid = [[1]]
输出：4

示例 3：
输入：grid = [[1,0]]
输出：4

提示：



为或

题解

这道题最牛逼的一点是你要想到，岛屿的周长就是岛屿方格和非岛屿方格相邻的边的数量（如下图所示）。也就是说，在DFS遍历中，从一个岛屿方格走向一个非岛屿方格，就将周长加1。
DFS_island_perimeter
所以，我们可以修改下网格DFS遍历的通用框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int dfsGrid(vector<vector<int>>& grid, int row, int col) {
  if (row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0) {
    // 从一个岛屿方格走向网格边界,周长加1
    return 1;
  }
  if (grid[row][col] == 0) {
    // 从一个岛屿方格走向水域方格,周长加1
    return 1;
  }
  if (grid[row][col] != 1) {
    // 过滤掉已经遍历过的
    return 0;
  }

  grid[row][col] = 2;  // 去重,防止多次遍历
  int res = dfsGrid(grid, row - 1, col) + dfsGrid(grid, row + 1, col) +
            dfsGrid(grid, row, col - 1) + dfsGrid(grid, row, col + 1);
  return res;
}

题目限制只有一个岛屿，那我们计算一个即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
 public:
  int islandPerimeter(vector<vector<int>>& grid) {
    for (int i = 0; i < grid.size(); i++) {
      for (int j = 0; j < grid[0].size(); j++) {
        if (grid[i][j] == 1) {
          return dfsGrid(grid, i, j);
        }
      }
    }
    return 0;
  }

  int dfsGrid(vector<vector<int>>& grid, int row, int col) {
    if (row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0) {
      // 从一个岛屿方格走向网格边界,周长加1
      return 1;
    }
    if (grid[row][col] == 0) {
      // 从一个岛屿方格走向水域方格,周长加1
      return 1;
    }
    if (grid[row][col] != 1) {
      // 过滤掉已经遍历过的
      return 0;
    }

    grid[row][col] = 2;  // 去重,防止多次遍历
    int res = dfsGrid(grid, row - 1, col) + dfsGrid(grid, row + 1, col) +
              dfsGrid(grid, row, col - 1) + dfsGrid(grid, row, col + 1);
    return res;
  }
};

三、岛屿的最大面积（中）

题目

给你一个大小为m x n的二进制矩阵grid。
岛屿是由一些相邻的1(代表土地) 构成的组合，这里的「相邻」要求两个1必须在水平或者竖直的四个方向上相邻。你可以假设grid的四个边缘都被0（代表水）包围着。
岛屿的面积是岛上值为1的单元格的数目。
计算并返回grid中最大的岛屿面积。如果没有岛屿，则返回面积为0。

示例 1：
max-area-of-island
输入：
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：
输入：
输出：0

提示：



为或

题解

从上面两道我们已经知道怎么计算岛屿数量和一个岛屿的周长，这道题是结合了上面两道。
因此我们可以对每个岛屿计算它的面积，最后返回最大的那个面积即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
 public:
  int maxAreaOfIsland(vector<vector<int>>& grid) {
    int res = 0;
    for (int i = 0; i < grid.size(); i++) {
      for (int j = 0; j < grid[0].size(); j++) {
        if (grid[i][j] == 1) {
          res = max(dfsGrid(grid, i, j), res);
        }
      }
    }
    return res;
  }

  int dfsGrid(vector<vector<int>>& grid, int row, int col) {
    if (row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0) {
      // row和col越界,都不算岛屿中的陆地,面积为0
      return 0;
    }
    if (grid[row][col] != 1) {
      // 遍历到海洋或者已经遍历过的陆地,面积为0
      return 0;
    }

    grid[row][col] = 2;  // 去重,防止多次遍历
    int res = dfsGrid(grid, row - 1, col) + dfsGrid(grid, row + 1, col) +
              dfsGrid(grid, row, col - 1) + dfsGrid(grid, row, col + 1) +
              1;  // 加1是因为第一次肯定是一块陆地才进来的dfsGrid
    return res;
  }
};

四、最大人工岛（困）

题目

给你一个大小为n x n二进制矩阵grid。最多只能将一格0变成1。
返回执行此操作后，grid中最大的岛屿面积是多少？
岛屿由一组上、下、左、右四个方向相连的1形成。

示例 1:
输入:
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2:
输入:
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:
输入:
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。  

提示：



为或

题解

这道题是第三题的升级版，现在我们可以将一个海洋变成陆地，从而连接两个岛屿。
那我们就需要先统计各个岛屿面积，找到最大的岛屿；然后把一个海洋变成陆地，再统计一遍连接后各个岛屿面积，找到最大的岛屿。

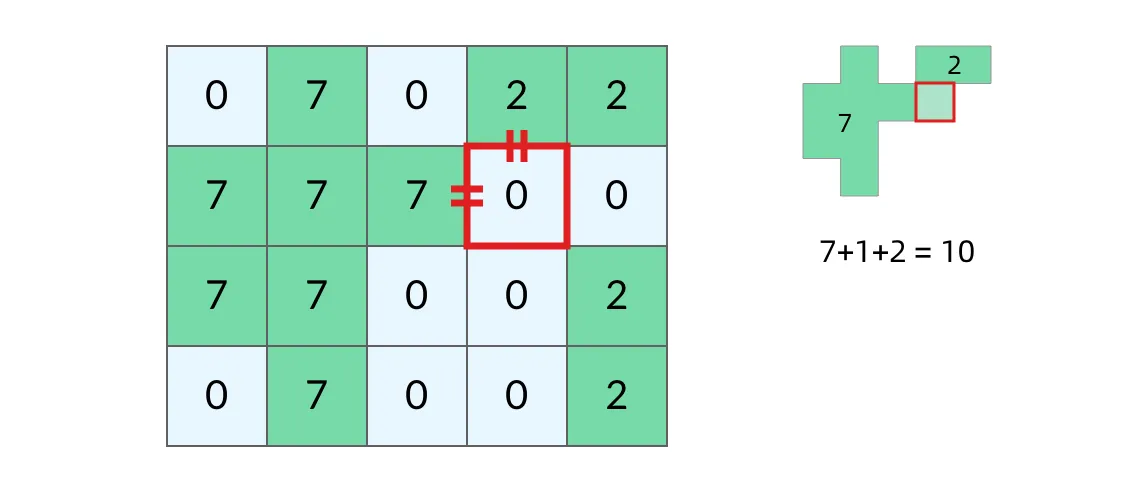
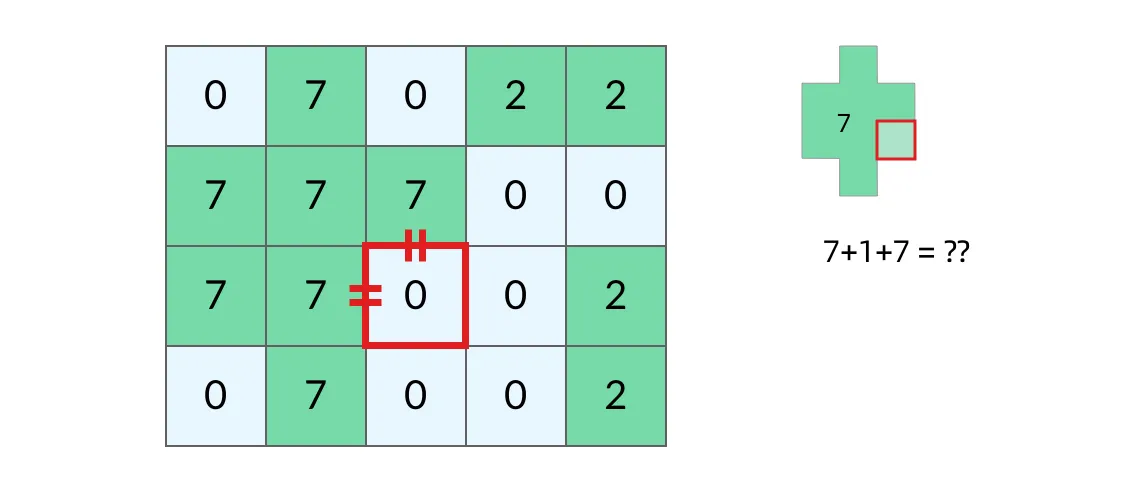
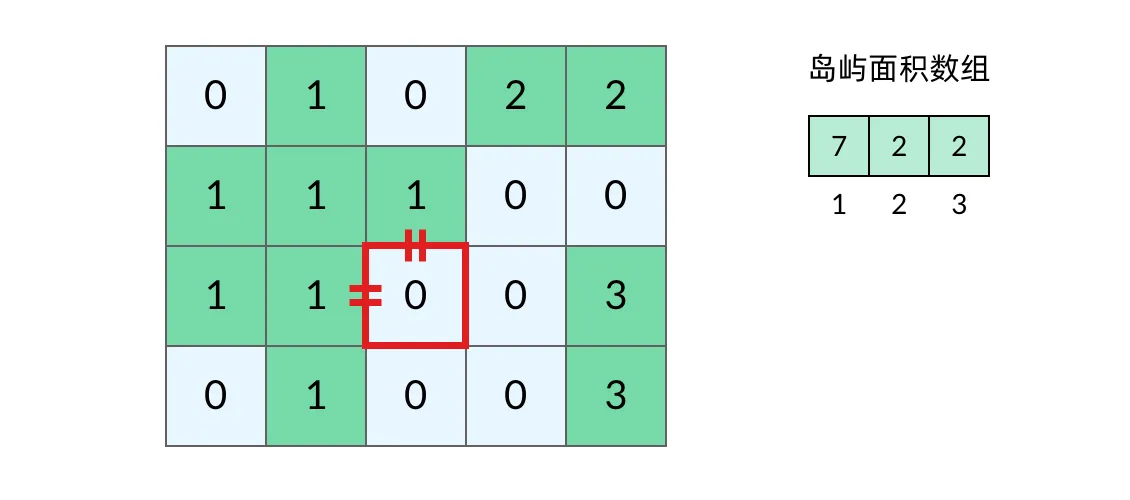
因此需要两次DFS遍历：
1、划分岛屿，给每个岛屿标号
标号要标什么呢？假设我们在所有的格子上标记出岛屿的面积。然后搜索哪个海洋格子相邻的两个岛屿面积最大。
例如下图中红色方框内的海洋格子，上边、左边都与岛屿相邻，我们可以计算出它变成陆地之后可以连接成的岛屿面积为7 + 1 + 2 = 10。
DFS_large_island_1
然而，这种做法可能遇到一个问题。如下图中红色方框内的海洋格子，它的上边、左边都与岛屿相邻，这时候连接成的岛屿面积难道是7 + 1 + 7 = 15？显然不是。这两个7来自同一个岛屿，所以填海造陆之后得到的岛屿面积应该只有7 + 1 = 8。
DFS_large_island_2
可以看到，要让算法正确，我们得能区分一个海洋格子相邻的两个7是不是来自同一个岛屿。那么，我们不能在方格中标记岛屿的面积，而应该用map记录每个岛屿面积，给每个岛屿标记map的key。
如下图所示。这样我们就可以发现红色方框内的海洋格子，它的两个相邻的岛屿实际上是同一个。
DFS_large_island_3

2、填充海洋，连接四周的岛屿
和上面类似，要遍历每个海洋格子上下左右的格子。又因为我们已经有map来记录了各个岛屿的面积，所以只需要在遍历时发现是岛屿，加上对应的面积即可，不需要再全部遍历该岛屿的陆地。
要注意的是，我们是将一个海洋变为陆地，所以海洋会占一个面积。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
class Solution {
 public:
  unordered_map<int, int> area;  // 存放各岛屿面积

 public:
  int largestIsland(vector<vector<int>>& grid) {
    int res = 0;
    int index = 2;  // 从2开始是为了和陆地的1做区分,防止多次遍历
    // 不同岛屿用不同的数字标记,统计各岛屿面积,同时记录最大值
    for (int i = 0; i < grid.size(); i++) {
      for (int j = 0; j < grid[0].size(); j++) {
        if (grid[i][j] == 1) {
          area[index] = dfsGrid(grid, i, j, index);
          res = max(res, area[index]);
          index++;
        }
      }
    }
    // 连接岛屿
    for (int i = 0; i < grid.size(); i++) {
      for (int j = 0; j < grid.size(); j++) {
        if (grid[i][j] == 0) {
          res = max(res, linkland(grid, i, j));
        }
      }
    }
    return res;
  }

  int dfsGrid(vector<vector<int>>& grid, int row, int col, int index) {
    if (row >= grid.size() || col >= grid[0].size() || row < 0 || col < 0) {
      return 0;
    }
    if (grid[row][col] != 1) {
      return 0;
    }

    grid[row][col] = index;
    int res = dfsGrid(grid, row - 1, col, index) +
              dfsGrid(grid, row + 1, col, index) +
              dfsGrid(grid, row, col - 1, index) +
              dfsGrid(grid, row, col + 1, index) + 1;
    return res;
  }

  int linkland(vector<vector<int>>& grid, int row, int col) {
    unordered_set<int> around;
    int linkarea = 1;  // 海洋占一个面积
    if (row - 1 >= 0 && grid[row - 1][col] > 1) {
      // 左
      around.insert(grid[row - 1][col]);
    }
    if (row + 1 < grid.size() && grid[row + 1][col] > 1) {
      // 右
      around.insert(grid[row + 1][col]);
    }
    if (col - 1 >= 0 && grid[row][col - 1] > 1) {
      // 上
      around.insert(grid[row][col - 1]);
    }
    if (col + 1 < grid.size() && grid[row][col + 1] > 1) {
      // 下
      around.insert(grid[row][col + 1]);
    }
    for (auto i : around) {
      linkarea += area[i];
    }
    return linkarea;
  }
};
License

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

Share

快来参与讨论吧~

BlogCategoriesTagsArchives
ProjectIMU_PreintegrationLeGO_LOAM
SocialFriendCircleCommentsTravelling
MoreHomePageAbout
©2018 - Felicx 使用 Stellar 创建
总访问 113701 次 | 本页访问 326 次
共发表 83 篇Blog · 总计 127.5k 字