前言

回溯算法本质是一个暴力穷举的过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”（即回退），尝试别的路径。

回溯法有“通用解题法”之称。它适合于解一些组合数较大的最优化问题。同时涉及回溯算法的题目都有一个共同点：列出所有满足的情况。

另外，基本所有能用回溯算法解决的题目总能画出一个二叉树来。我们称这样的树为决策树。解决一个回溯问题，其实就是一个决策树的遍历过程。所以在回溯法中，深度优先搜索是一种很重要的工具。

算法框架

遍历整个决策树时，你只需要思考三个问题：

路径：你已经做出的选择
选择列表：也就是你当前可以做的选择
结束条件：到达决策树底层，无法再做选择的条件

以『全排列』为例。我们可以直接画出全排列的决策树如下：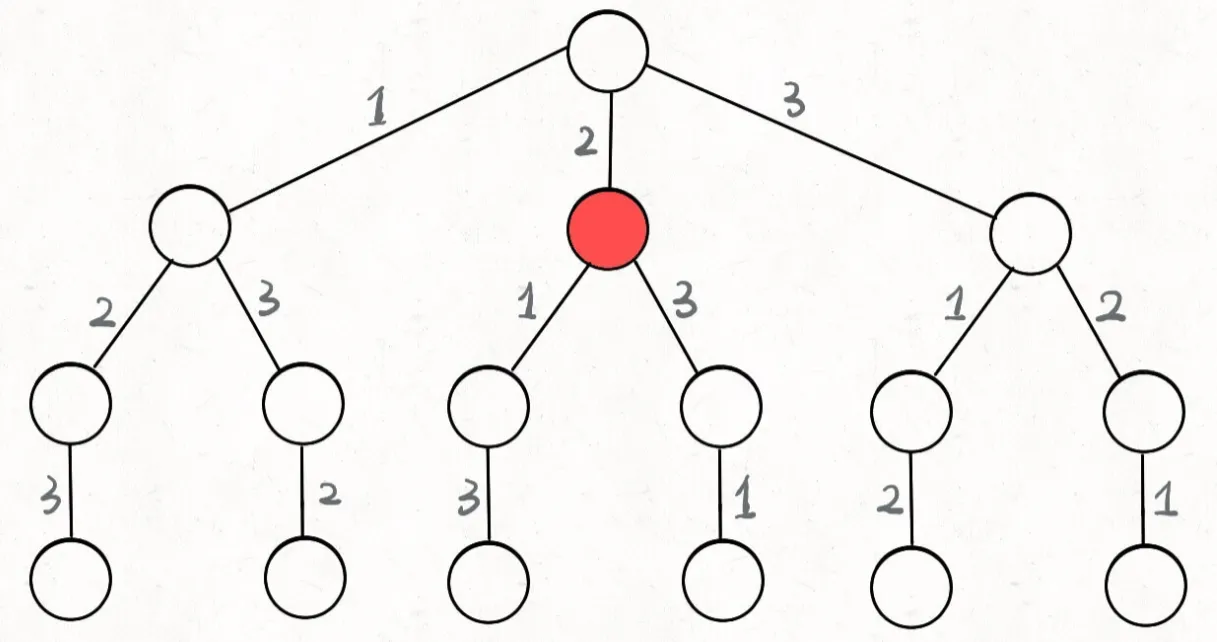

根据这个决策树，比如说你站在红色节点上。你可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在你⾝后，这个选择你之前做过了，而全排列是不允许重复使用数字的。

所以在这里：
[2] 就是「路径」，记录你已经做过的选择；
[1,3] 就是「选择列表」，表示你当前可以做出的选择；
遍历到树的底层，即选择列表为空的时候就是「结束条件」。

框架如下：

result = []
def backtrack(原数组, 行数):
  if 满足结束条件:
    result.add(路径)
    return

  for 选择 in 选择列表:
    # 做选择判断,排除不合法的选择
    continue
    # 将合法的选择加⼊选择列表
    路径.add(选择)
    # 回溯下一行
    backtrack(原数组, 行数+1)
    # 撤销选择,将该选择从选择列表移除
    路径.remove(选择)

上面的框架中，为什么要撤销选择呢
前面我们就说过，回溯算法本质就是在遍历决策树。大家可以想一想，你的一次选择结束了，你肯定要返回当当时进入递归时的状态，然后进行另外的选择啊，不然你不返回状态，其他选择怎么办。如果不撤销，按照下图的角度，你只会得到一个结果，就是用于遍历的左子树。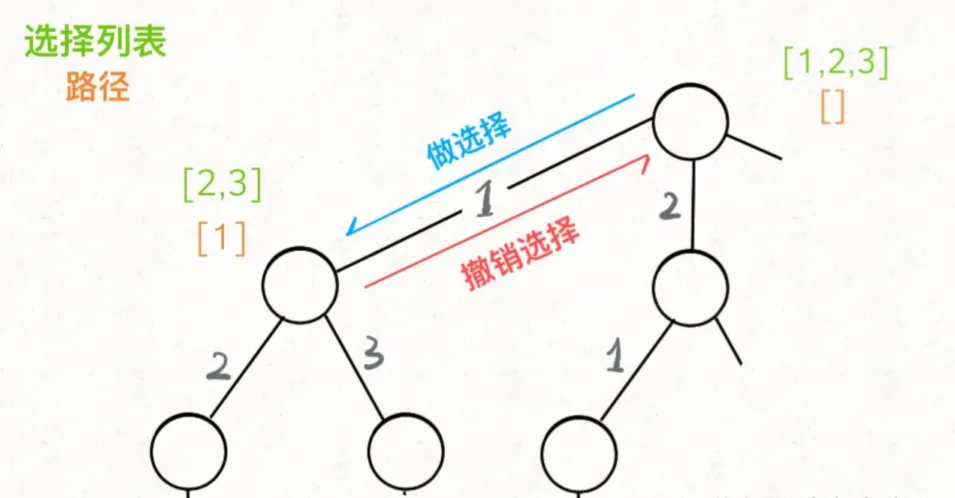

代码示例

class Solution {
 private:
  vector<vector<int>> result;  // 存储结果
  vector<int> track;           // 存储当前路径

 public:
  vector<vector<int>> permute(vector<int>& nums) {
    backtrack(nums, 0);  // 回溯函数
    return result;
  }

  // 路径：记录在 track 中
  // 选择列表：nums 中不存在于 track 中的元素
  // 结束条件：遍历完所有行, 即 index = nums.size()
  void backtrack(vector<int>& nums, int index) {
    if (index == nums.size()) {
      result.push_back(track);
      return;
    }

    for (int i = 0; i < nums.size(); i++) {
      if (find(track.begin(), track.end(), nums[i]) != track.end()) {
        // 排除不合法的选择
        continue;
      }
      track.push_back(nums[i]);  // 做选择,将当前元素添加到路径中
      backtrack(nums, index + 1);  // 进⼊下⼀层决策树
      track.pop_back();  // 撤销选择,将当前元素从路径中弹出
    }
  }
};