一、合并两个有序链表（简）

题目

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

graph LR
  a((1)) --> b((2)) --> c((4))
graph LR
  d[1] --> e[3] --> f[4]
graph LR
  a((1)) --> d[1] --> b((2)) --> e[3] --> c((4)) --> f[4]

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：
输入：l1 = [], l2 = []
输出：[]

示例 3：
输入：l1 = [], l2 = [0]
输出：[0]

提示：
两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

题解

很简单，定义第三个链表，然后依次比较两个有序链表的每一位，小的先接到第三个链表后面。
最后遍历完后，如果两个链表中还有剩下元素的，直接整个接到第三个链表后面。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
 public:
  ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    ListNode* dummyNode = new ListNode(0);
    ListNode* pre = dummyNode;
    while (l1 != NULL && l2 != NULL) {
      if (l1->val <= l2->val) {
        pre->next = l1;
        l1 = l1->next;
      } else {
        pre->next = l2;
        l2 = l2->next;
      }
      pre = pre->next;
    }
    if (l1 == NULL) {
      pre->next = l2;
    } else if (l2 == NULL) {
      pre->next = l1;
    }
    return dummyNode->next;
  }
};

二、合并K个升序链表（困）

题目

给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：
输入：lists = [ [1,4,5],[1,3,4],[2,6] ]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：
输入：lists = [ ]
输出：[ ]

示例 3：
输入：lists = [ [ ] ]
输出：[ ]

提示：
k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10^4

题解1

根据之前的合并两个有序链表，遍历链表组中的元素，两两合并即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
 public:
  ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    ListNode* dummyNode = new ListNode(0);
    ListNode* pre = dummyNode;
    while (l1 != NULL && l2 != NULL) {
      if (l1->val <= l2->val) {
        pre->next = l1;
        l1 = l1->next;
      } else {
        pre->next = l2;
        l2 = l2->next;
      }
      pre = pre->next;
    }
    if (l1 == NULL) {
      pre->next = l2;
    } else if (l2 == NULL) {
      pre->next = l1;
    }
    return dummyNode->next;
  }

  ListNode* mergeKLists(const vector<ListNode*>& lists) {
    if (lists.size() == 0) {
      return NULL;
    }
    ListNode* result = NULL;
    for (int i = 0; i < lists.size(); i++) {
      result = mergeTwoLists(result, lists[i]);
    }
    return result;
  }
};

题解2

题解1是按顺序合并，每次合并完的链表就会加长，下一次合并又得遍历一遍，所以时间复杂度会高。
这里可以联想到排序算法的归并排序。当然这里我们不用排序，只用归并，然后一一合并链表。具体怎么做呢。
比如lists=[[1, 2], [3, 4], [5, 6], [7, 8]]，首先拆分成[[1, 2], [3, 4]]和[[5, 6], [7, 8]]，然后两组分别组内合并，得到两个链表，再互相合并。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
 public:
  ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    ListNode* dummyNode = new ListNode(0);
    ListNode* pre = dummyNode;
    while (l1 != NULL && l2 != NULL) {
      if (l1->val <= l2->val) {
        pre->next = l1;
        l1 = l1->next;
      } else {
        pre->next = l2;
        l2 = l2->next;
      }
      pre = pre->next;
    }
    if (l1 == NULL) {
      pre->next = l2;
    } else if (l2 == NULL) {
      pre->next = l1;
    }
    return dummyNode->next;
  }

  ListNode* merge(const vector<ListNode*>& lists, int left, int right) {
    if (left == right) {
      return lists[left];
    }
    if (left > right) {
      return NULL;
    }
    int mid = (left + right) >> 1;
    ListNode* l1 = merge(lists, left, mid);
    ListNode* l2 = merge(lists, mid + 1, right);
    return mergeTwoLists(l1, l2);
  }

  ListNode* mergeKLists(const vector<ListNode*>& lists) {
    if (lists.size() == 0) {
      return NULL;
    }
    return merge(lists, 0, lists.size() - 1);
  }
};

题解3

因为最后返回的链表中数组是按由小到大排序的，而C++自带的优先队列priority_queue，可以自动帮我们排序。
所以可以拿小根堆先遍历参数中的lists, 因为小根堆top()返回的是最小值，因此可以通过不断吐出小根堆的值，重新组装链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
 public:
  ListNode* mergeKLists(vector<ListNode*>& lists) {
    ListNode* res = new ListNode();
    // 小根堆
    priority_queue<int, vector<int>, greater<int>> queue;
    for (auto list : lists) {
      while (list != NULL) {
        queue.push(list->val);
        list = list->next;
      }
    }
    ListNode* temp = res;
    while (!queue.empty()) {
      ListNode* node = new ListNode();
      node->val = queue.top();
      queue.pop();
      temp->next = node;
      temp = temp->next;
    }
    return res->next;
  }
};

题解4

题解3用的是C++自带的priority_queue，我们也可以自己定义类似的queue，从小到大排序。

1
2
3
4
5
struct Status {
  int val;
  ListNode* ptr;
  bool operator<(const Status& rhs) const { return val > rhs.val; }
};

其余的和题解3类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
 public:
  ListNode* mergeKLists(vector<ListNode*>& lists) {
    struct Status {
      int val;
      ListNode* ptr;
      bool operator<(const Status& rhs) const { return val > rhs.val; }
    };

    ListNode* res = new ListNode();
    // 最小堆
    priority_queue<Status> queue;
    for (auto list : lists) {
      while (list != NULL) {
        queue.push({list->val, list});
        list = list->next;
      }
    }
    ListNode* temp = res;
    while (!queue.empty()) {
      ListNode* node = new ListNode();
      node->val = queue.top().val;
      queue.pop();
      temp->next = node;
      temp = temp->next;
    }
    return res->next;
  }
};

三、相交链表（简）

题目

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
图示两个链表在节点 c1 开始相交：

graph LR
  a1 --> a2 --> c1
  b1 --> b2 --> b3 --> c1 --> c2 --> c3

题目数据 保证 整个链式结构中不存在环。
注意，函数返回结果后，链表必须 保持其原始结构 。
自定义评测：
评测系统 的输入如下（你设计的程序 不适用 此输入）：

  • intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
  • listA - 第一个链表
  • listB - 第二个链表
  • skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
  • skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

graph LR
  a[4] --> b[1] --> 8
  d[5] --> 6 --> e[1] --> 8 --> f[4] --> g[5]

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at ‘8’
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

graph LR
  a[1] --> 9 --> b[1] --> 2
  3 --> 2 --> 4

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at ‘2’
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

graph LR
  2 --> 6 --> 4
  1 --> 5

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：
listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 10^4
1 <= Node.val <= 10^5
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

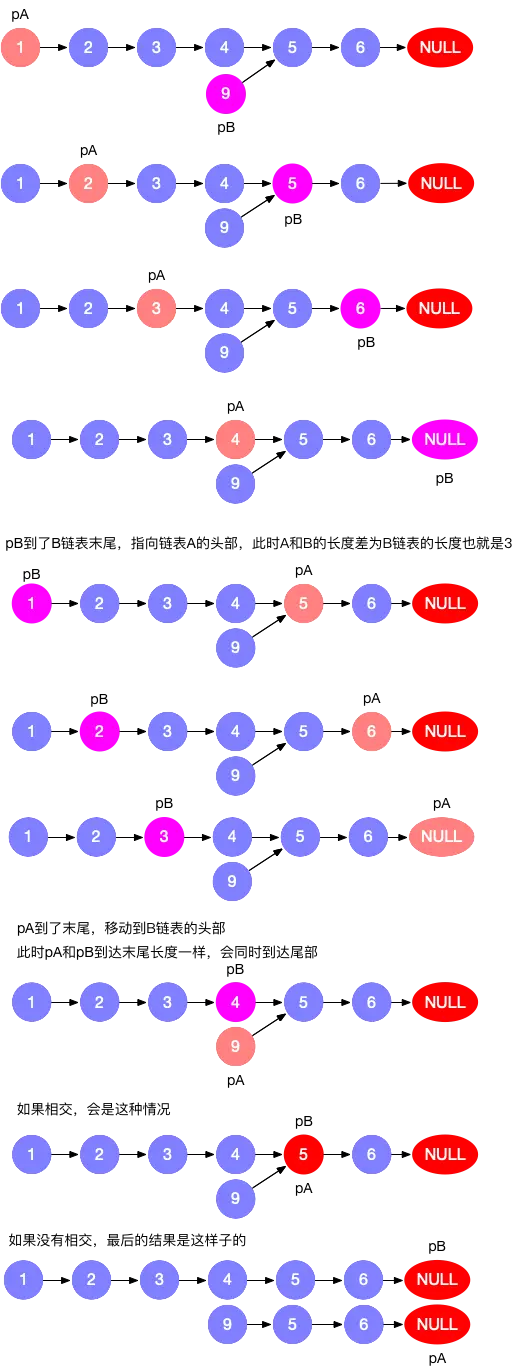
题解

直接看图更好理解，
1、指针 pA 指向 A 链表，指针 pB 指向 B 链表，依次往后遍历；
2、如果 pA 到了末尾，则 pA = headB 继续遍历；
3、如果 pB 到了末尾，则 pB = headA 继续遍历；
4、比较长的链表指针指向较短链表head时，长度差就消除了；
5、如此，只需要将最短链表遍历两次，当 pA = pB 时，即找到位置。
Intersection_linked_list

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
 public:
  ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
    if (headA == NULL || headB == NULL) {
      return NULL;
    }
    ListNode *pA = headA, pB = headB;
    while (pA != pB) {
      pA = (pA == NULL) ? headB : pA->next;
      pB = (pB == NULL) ? headA : pB->next;
    }
    return pA;
  }
};

四、重排链表（中）

题目

给定一个单链表 L 的头节点 head ，单链表 L 表示为：
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为：
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1：
输入：head = [1,2,3,4]
输出：[1,4,2,3]

示例 2：
输入：head = [1,2,3,4,5]
输出：[1,5,2,4,3]

提示：
链表的长度范围为 [1, 5 * 10^4]
1 <= node.val <= 1000

题解

这题其实是个大杂烩，寻找链表中点(快慢指针) + 链表逆序（反转链表） + 合并链表，这三个的合集。

举个例子，链表 1 -> 2 -> 3 -> 4 -> 5 -> 6
第一步，将链表平均分成两半
1 -> 2 -> 3
4 -> 5 -> 6
第二步，将第二个链表逆序
1 -> 2 -> 3
6 -> 5 -> 4
第三步，依次连接两个链表，得到答案
1 -> 6 -> 2 -> 5 -> 3 -> 4

第一步找中点的话，很明显用快慢指针。快指针一次走两步，慢指针一次走一步，当快指针走到终点的话，慢指针会刚好到中点。如果节点个数是偶数的话，slow 走到的是左端点，利用这一点，我们可以把奇数和偶数的情况合并，不需要分开考虑。（快慢指针参考环形链表问题）

第二步链表逆序的话，有迭代和递归的两种方式，迭代的话主要利用两个指针，依次逆转。（反转链表参考反转链表问题）

第三步的话就很简单了，两个指针分别向后移动就可以。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
 public:
  void reorderList(ListNode* head) {
    if (head == NULL || head->next == NULL)
      return;

    // 快慢指针分出两段
    ListNode* slow = head;
    ListNode* fast = head;
    while (fast->next && fast->next->next) {
      slow = slow->next;
      fast = fast->next->next;
    }

    // 后端反转
    ListNode* reverseNode = slow->next;
    slow->next = NULL;
    reverseNode = reverseList(reverseNode);

    // 合并链表
    while (reverseNode) {
      ListNode* tempHead = head->next;
      ListNode* tempReverse = reverseNode->next;
      head->next = reverseNode;
      reverseNode->next = tempHead;
      head = tempHead;
      reverseNode = tempReverse;
    }
  }

  ListNode* reverseList(ListNode* head) {
    ListNode* next = NULL;
    ListNode* prev = NULL;
    while (head) {
      next = head->next;
      head->next = prev;
      prev = head;  // prev 移动
      head = next;  // head 移动
    }
    return prev;
  }
};

五、排序链表（中）

题目

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

示例 1：

graph LR
  4 --> 2 --> 1 --> 3

—>

graph LR
  1 --> 2 --> 3 --> 4

输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

graph LR
  -1 --> 5 --> 3 --> 4 --> 0

—>

graph LR
  -1 --> 0 --> 3 --> 4 --> 5

输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：
输入：head = []
输出：[]

提示：
链表中节点的数目在范围 内

需要在时间复杂度和常数级空间复杂度下，对链表进行排序

题解1

要实现时间复杂度和常数级空间复杂度，看之前的排序算法可以知道，符合要求的只有快速排序和归并排序。

首先是快速排序，回顾数组的快排步骤：
1、确定一个分界点；
2、调整区间：使得左边所有值 <= 分界点， 右边所有值 >= 分界点；
3、递归处理左右两段。

那么链表也可以同样的操作：
1、首先找到链表的中间节点；
2、然后将链表分为左、中、右三部分，分别存储在三个链表中；
3、然后递归地对左、右链表进行排序；
4、最后将左、中、右三个链表拼接起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class Solution {
 public:
  ListNode* sortList(ListNode* head) {
    // 如果链表为空或只有一个节点，直接返回
    if (!head || !head->next) {
      return head;
    }

    // 定义左右指针和中间节点
    ListNode *left = new ListNode(0), *right = new ListNode(0),
             *mid = new ListNode(0);
    ListNode *i = left, *j = right, *m = mid;

    // 这里用中间节点的原因是，如果每次用最左边的节点，对于纯递增和纯递减的case就退化为O(n)
    int pivot = getMid(head)->val;
    // 如果不考虑超时限制，也可以取最左边的节点作为中间节点
    // int pivot = head->val;

    // 遍历链表，将节点分别放入左、右、中间链表中
    ListNode* cur = head;
    while (cur) {
      if (cur->val < pivot) {
        i->next = cur;
        i = i->next;
      } else if (cur->val > pivot) {
        j->next = cur;
        j = j->next;
      } else {
        m->next = cur;
        m = m->next;
      }
      cur = cur->next;
    }

    // 将左、右链表的末尾指向空
    i->next = j->next = m->next = NULL;

    // 递归排序左、右链表
    left->next = sortList(left->next);
    right->next = sortList(right->next);

    // 将左、中、右链表拼接起来
    cur = left;
    while (cur->next) {
      cur = cur->next;
    }
    cur->next = mid->next;
    while (cur->next) {
      cur = cur->next;
    }
    cur->next = right->next;

    // 返回排序后的链表
    return left->next;
  }

  ListNode* getMid(ListNode* head) {
    ListNode* fast = head;
    ListNode* slow = head;
    while (fast != nullptr && fast->next != nullptr) {
      fast = fast->next->next;
      slow = slow->next;
    }
    return slow;
  }
};

题解2

上面说了，归并也可以解决这道题。
回顾数组的归并步骤：
1、确定分界点mid = (left + right)>>1，逐层折半分组；
2、然后从最小分组开始比较排序，合并成一个大的分组，逐层进行

那么链表也可以同样的操作：
1、用快慢指针的方法找到链表的中间节点；
2、然后递归地对前半部分和后半部分分别进行排序；
3、最后将两个有序链表合并起来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
 public:
  ListNode* sortList(ListNode* head) {
    if (!head || !head->next)
      return head;  // 如果链表为空或只有一个节点，直接返回
    ListNode *slow = head, *fast = head;  // 定义快慢指针
    while (fast->next && fast->next->next) {
      // 快指针每次走两步，慢指针每次走一步，最终慢指针指向链表中间节点
      slow = slow->next;
      fast = fast->next->next;
    }
    fast = slow->next;  // 定义fast指针指向链表后半部分
    slow->next = NULL;  // 将链表断开
    return merge(sortList(head), sortList(fast));
    // 递归调用sortList函数，对前半部分和后半部分分别进行排序，然后合并两个有序链表
  }

  ListNode* merge(ListNode* l1, ListNode* l2) {  // 合并两个有序链表
    // 定义虚拟头节点和当前节点
    ListNode *dummy = new ListNode(0), *cur = dummy;
    while (l1 && l2) {          // 当l1和l2都不为空时
      if (l1->val < l2->val) {  // 如果l1的值小于l2的值
        cur->next = l1;         // 将l1接到当前节点的后面
        l1 = l1->next;          // l1指针后移
      } else {                  // 如果l1的值大于等于l2的值
        cur->next = l2;         // 将l2接到当前
        l2 = l2->next;          // l2指针后移
      }
      cur = cur->next;  // 当前节点后移
    }
    cur->next = l1 ? l1 : l2;  // 将剩余的链表接到当前节点的后面
    return dummy->next;        // 返回虚拟头节点的下一个节点
  }
};

六、删除排序链表中的重复元素（简）

题目

给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。

示例 1：

graph LR
  a(1) --> b(1) --> c(2)

—>

graph LR
  a(1) --> b(2)

输入：head = [1,1,2]
输出：[1,2]

示例 2：

graph LR
  a(1) --> b(1) --> c(2) --> d(3) --> e(3)

—>

graph LR
  a(1) --> b(2) --> c(3)

输入：head = [1,1,2,3,3]
输出：[1,2,3]

提示：

  • 链表中节点数目在范围 [0, 300] 内
  • -100 <= Node.val <= 100
  • 题目数据保证链表已经按升序 排列

题解

1、首先，使用虚拟头结点dummyNode，让它的next指针指向head，这样可以避免对head进行特判；
2、然后遍历链表，有重复元素head就跳一位，就可以达到去重目的了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
 public:
  ListNode* deleteDuplicates(ListNode* head) {
    ListNode* dummyNode = new ListNode(0);
    dummyNode->next = head;
    while (head) {
      while (head->next && head->val == head->next->val) {
        head->next = head->next->next;
      }
      head = head->next;
    }
    return dummyNode->next;
  }
};

七、删除排序链表中的重复元素II（中）

题目

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

示例 1：

graph LR
  a(1) --> b(2) --> c(3) --> d(3) --> e(4) --> f(4) --> g(5)

—>

graph LR
  a(1) --> b(2) --> c(5)

输入：head = [1,2,3,3,4,4,5]
输出：[1,2,5]

示例 2：

graph LR
  a(1) --> b(1) --> c(1) --> d(2) --> e(3)

—>

graph LR
  a(2) --> b(3)

输入：head = [1,1,1,2,3]
输出：[2,3]

提示：
链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序 排列

题解

跟上面第六题类似，只不过这里所有重复的都删除，不保留。
1、可以用个标志位，判断当前节点是否需要删除；
2、遍历链表，有重复节点就将head右移，这样head就指向了重复节点中的最后一个，同时标记该节点为要删除的；
3、根据flag进行删除即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
 public:
  ListNode* deleteDuplicates(ListNode* head) {
    ListNode* dummyNode = new ListNode(0);
    dummyNode->next = head;
    ListNode* pre = dummyNode;
    while (head) {
      bool flag = false;  // 标记当前节点是否需要删除
      while (head->next && head->val == head->next->val) {
        head = head->next;
        flag = true;  // 标记当前节点需要删除
      }
      if (flag) {
        // 对于要删除的节点，将前一个节点的next指针指向当前节点的下一个节点，这样就可以将当前节点删除
        pre->next = head->next;
      } else {
        // 如果当前节点不用删除，则pre不需要改变指向，仍然指向当前节点的前一个节点
        pre = head;
      }
      head = head->next;
    }
    return dummyNode->next;
  }
};
License

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

Share

快来参与讨论吧~

BlogCategoriesTagsArchives
ProjectIMU_PreintegrationLeGO_LOAM
SocialFriendCircleCommentsTravelling
MoreHomePageAbout
©2018 - Felicx 使用 Stellar 创建
总访问 113701 次 | 本页访问 326 次
共发表 83 篇Blog · 总计 127.5k 字